Virgil and Arnaut, for
Adalinda Gasparini (a draft in
freestyle English)
 |
 |
Adalinda
Gasparini
wrote a fine paper on the French troubadour Arnaut, for
an international Dante
conference held in
Tan
m’abellis vostre cortes deman…
Formazione
amorosa come peregrinatio
& periclitatio
She
quotes the
first sestina
(sixtain) of Arnaut, an
intricate form of a poem invented by himself, and
explains the cledisat
or framework – returning
permutations and shifting rings of rime words – via an
elegant algorithm in
form of an Archimedean spiral. Arnaut may well have
influenced Dante who
mentions him toward the end of Purgatorio 26, where the
troubadour announces
himself in Provençal
Ieu
sui Arnaut
(I am Arnaut)
in
perfect
symmetry to an earlier Italian announcement
Io
son Virgilio (I
am Virgil)
at
the beginning
of Purgatorio 7. The Divina Commedia has 100 canti:
34
(Inferno) 33
(Purgatorio)
33 (Paradiso)
Virgil
and Arnaut
mark another partition of the one hundred canti:
40
20 40
40
canti
1-40
(Inferno 1-34, Purgatorio
1-6)
20
canti
41-60
(Purgatorio 7-26)
40
canti
61-100
(Purgatorio 27-33,
Paradiso 1-33)
Io
son Virgilio
seven lines into
canto 41
Ieu
sui Arnaut
seven lines before the
end of canto 60
The
partition 40
20 40 generates musical proportions:
40
/ 20
or 2/1 octave
40
+ 20 = 60
60 / 40
or 3/2 quint
40
+ 40 = 80
80 / 60
or 4/3 quart
4/3
times 3/2 equals 2/1
quart
and quint combined yield an octave
A
similar number game
leads from the partition 40 20 40 to the so-called Sacred Triangle
40
+ 20 = 60
40 + 40 = 80
40 + 20 + 40 = 100
60-80-100
being a multiple of
The
Sacred
Triangle
This
triples
generate a sequence of ever rounder polygons of 12 20 28
36 … sides (of two or
three different lengths per polygon, multiples of the
square roots of 2 and 5
or 2 times 5 that can be approximated by additive number
columns). The slowly
rounding polygons approximate the circle of radius 5 25
125 625 ... in the ever
finer grid 10 by 10, 50 by 50, 250 by 250, 1250 by 1250
…
Let
us imagine a
circle of radius 50 and diameter 100 in the grid 100 by
100, according to the
number of canti in the Divina Commedia. The crossing
horizontal and vertical
axes mark the center of the circle, while their ends
provide four points of the
circumference. The Sacred Triangle
Let
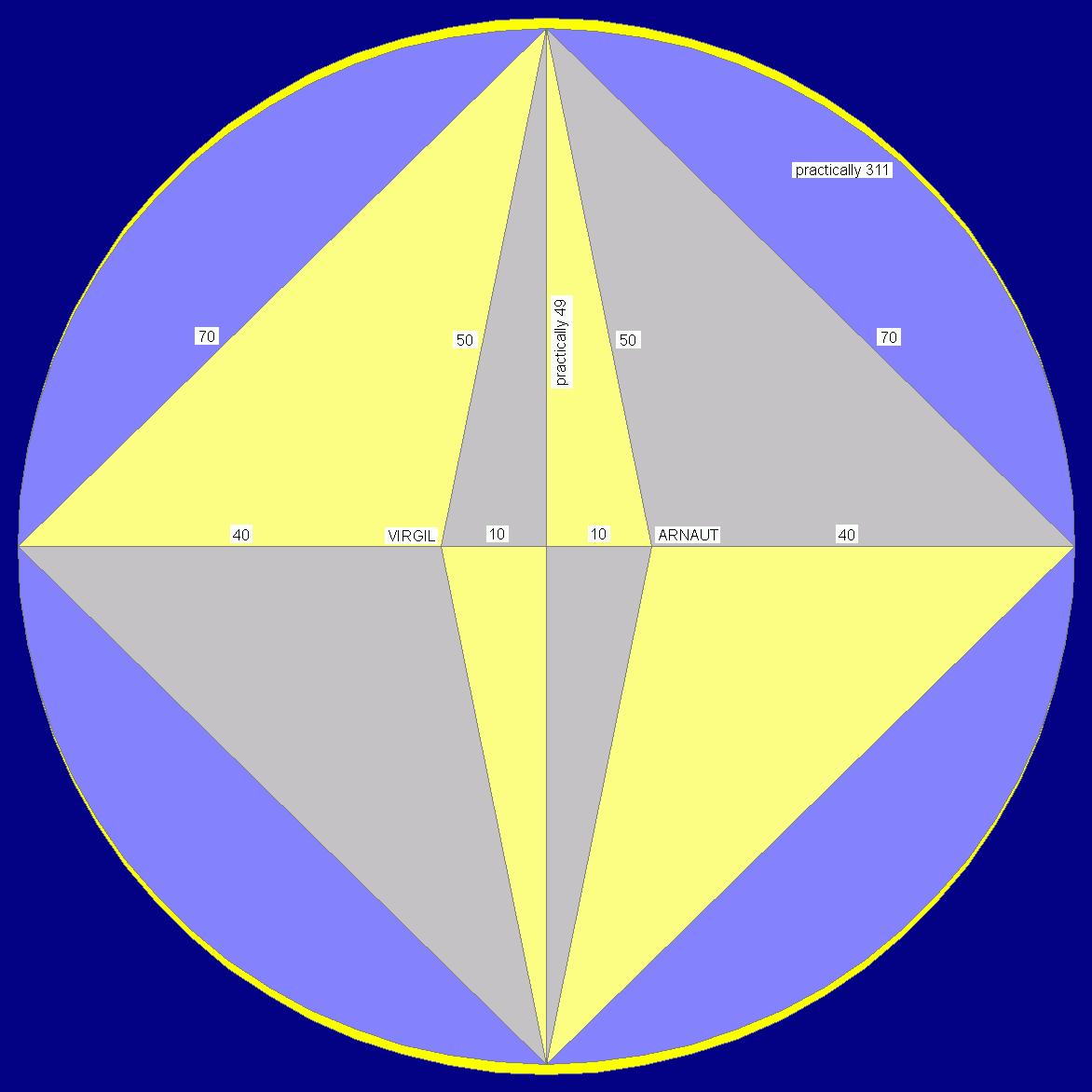
us imagine an
ellipse defined by the partition 40 20 40 as marked by
Virgil and Arnaut (click to enlarge)
 |
 |
This
ellipse has
remarkable numbers. The long horizontal axis measures
100 units and the
slightly shorter vertical one practically 98 units (49
plus 49). The side of
the inscribed rhomb, nearly a square, measures exactly
70 units, and the side
of the narrow vertical rhomb confined by the foci (focal
points) held by Virgil
and Arnaut measures exactly 50 units. Finally, the
circumference of the round
ellipse measures practically 311 units. From all the
ellipses of the long axis
100 only this one has such interesting numbers, integers
and near integers. (In
mathematical terms, the ellipse visualizes a whole
number solution of the
equation aa minus bb equals bb minus cc, namely, 70x70
minus 50x50 equals 50x50
minus 10x10.)
The
medieval
saying deus est
sphaera means that
God is present in the perfect form of the circle. A
sphere on paper, reduced by
one dimension, is a circle, still a perfect form. Let us
regard the imaginary
circle of diameter 100 as the circle of divine
perfection and knowledge and
truth, while the ellipse given by the partition 40 20 40
may symbolize the
Divina Commedia revolving around Virgil, whom Dante owns
his style (Inferno
1:85-87), and Arnaut who would have provided the seed of
inspiration, so to
say. The full circle stands for divine perfection, all
embracing knowledge and
absolute truth, whereas the ellipse, a round one almost
filling the circle,
represents the best of human work that comes close to
perfection and truth, but
only in way of better and better approximations, always
leaving a gap that
can’t be bridged, not even by the most perfect work of
art and most elegant
scientific theory, a principal gap holding surprises for
the future, new ideas
and theories to be found and developed by coming
generations. We can only
approach the truth, never really reach it. If you look
at a disk from an angle,
the circle is reduced to an ellipse. One dimension of
the circle is preserved,
the other reduced by a factor between one (full circle)
and zero (line). The
word ellipse goes back to the Greek and means wanting,
standing behind;
something is missing, left out, as in the elliptic way
of speaking. Our human
knowledge is elliptic: adequate in one dimension,
wanting in the other (or
another) dimension.
The
ellipse
defined by the 100 canti of the Divina Commedia and the
partition 40 20 40
marked by Virgil and Arnaut conveys a philosophical
message that goes along
with my cosmological interpretation of the Divina
Commedia. The long poem has
14,233 lines, one line short of the cosmological number
14,234 in Dante’s model
universe. One line is missing, the line of the divine
messenger that would complete
the epic, as each canto closes on a beautiful line of
poetic power. Only that
the one line to be delivered by the divine messenger
would transcend all human
wisdom. It is that single line we are working on,
generation for generation.
December
2, 2012,
Franz
Gnaedinger
Postscript.
An
example of symbolic geometry in an Italian painting,
Baptism of Christ, by
Piero della Francesca. The drawings may speak for
themselves
 |
 |
 |
 |