CLAUDIA CHELLINI E ADALINDA GASPARINI
|
PERCHÉ PENSARE A UNA GEOMETRIA DELLE FIABE? Perché pensare a una geometria delle fiabe soggiacente a ogni interpretazione, perché cercare di chiarire come ogni ermeneutica antica o moderna possa fornirne un'interpretazione convincente? Perché le favole sono dotate di un grado massimo di democrazia, che le fa viaggiare attraverso il tempo e lo spazio, fra bambini e adulti, fra finissimi letterati e narratori analfabeti? Cosa consente ai loro motivi di intrecciarsi, combinarsi, sciogliersi, fra oriente e occidente, alla corte del Re Sole o del Califfo Harun ar-Rashid come nei suq e nelle aie contadine? Perché possono essere uno strumento di grande valore nel lavoro di educazione e di cura? La loro docilità all'interpretazione è insieme la loro indipendenza dall'interpretazione stessa, e racconta qualcosa che ci accomuna: possiamo ascoltarle in modo da capire qualcosa di più della nostra mente, della nostra unicità che è simultaneamente la nostra comunanza? Il linguaggio della scienza è matematico. L'ipotesi che sta alla base di questa ricerca è che per capire la fiaba, intesa come una delle espressioni paradigmatiche della psiche individuale e collettiva, si possano cercare strumenti nel campo della matematica. Chi si dedica allo studio della complessità della realtà psichica, inaugurato da Sigmund Freud, può trovare in questa geometria qualitativa spunti e risonanze di grande valore. Per questo tentiamo di formalizzare le fiabe applicando un oggetto topologico, le trecce, sperando che i nostri modesti mezzi non costituiscano un impedimento insormontabile. Solo un approccio scientifico può evitare il rischio in cui cade, proprio quando ha successo, ogni sistema ermeneutico: spiegare obscura per obscuriora. Analogamente cade nella semplificazione priva di senso ogni interpretazione il cui fine è spiegare tutto: quando lo studioso completa la costruzione della sua gabbia interpretativa la fiaba è già volata via. La nostra formalizzazione intende il movimento trasformativo della fiaba come insieme di relazioni fra attanti, articolato in una sequenza temporale irreversibile. I diversi attanti, che possono essere intesi come personaggi schematici, significativi per la particolare cultura nella quale la fiaba viene scritta o narrata, corrispondono in chiave psicoanalitica a figure proprie della realtà psichica del soggetto che legge o ascolta. Abbiamo distinto quattro tipi di attanti, due per le figure genitoriali, due per le figure filiali. Ogni fiaba racconta di un attante protagonista, maschile o femminile, in ogni caso in posizione filiale, che intreccia il suo percorso con le figure parentali, nella maggior parte dei casi sia maschili che femminili, in certi casi con altre figure filiali maschili o femminili, e, se e solo se la fiaba finisce con le nozze regali, con una figura filiale del genere opposto al suo. Ogni personaggio si iscrive pertanto in una di queste quattro tipologie attanziali, a seconda della funzione che svolge in relazione all'attante protagonista della fiaba, che a sua volta appartiene, come già detto, alla tipologia filiale femminile o maschile. In questa pagina si dà una breve descrizione degli intrecci che geometrizzano le relazioni fra attanti, presentando a titolo di esempio una parte delle trecce di una sola favola, la più famosa del mondo, nella versione più antica: La gatta Cennerentola. Si propongono in questo sito le formalizzazioni complete di questa versione (Basile, 1634) e di altre tre Cenerentole particolarmente significative (Perrault, 1697; Grimm, 1812; Disney, 1950), accessibili anche dalla home page. Queste trecce sono corredate da didascalie che si attivano scorrendo con il mouse e dai testi integrali delle fiabe. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
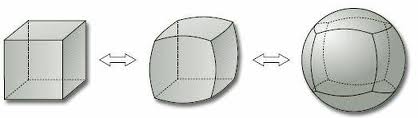
1. GEOMETRIA TOPOLOGICA La topologia è una geometria che studia le proprietà che definiscono forme e figure nello spazio indipendentemente dalle loro misure. Ha grande importanza nel campo della geometria e della matematica, ed è feconda di riflessioni e applicazioni per la scienza contemporanea. Si possono immaginare gli oggetti di questa geometria non euclidea come fatti di gomma o di pasta, illimitatamente estensibili e comprimibili: le dimensioni e la forma degli oggetti possono mutare altrettanto illimitatamente. La geometria topologica differisce dalla geometria euclidea, comunemente studiata a scuola, perché non è quantitativa ma qualitativa: in geometria topologica le dimensioni degli oggetti sono insignificanti. La difficoltà che si incontra nel comprendere la natura degli oggetti topologici consiste nella resistenza ad abbandonare il senso di padronanza che le misure sostengono, privilegiando la vista, che consente un grado di astrazione maggiore rispetto agli altri sensi. Comprendere gli oggetti topologici, con le loro equivalenze e le loro non equivalenze, richiede che sia attiva una percezione diversa da quella richiesta per il riconoscimento delle equivalenze e delle differenze fra oggetti della geometria euclidea: un bambino piccolo e un cieco dalla nascita distinguono più facilmente la differenza fra una sfera e un toro (FIGURA 2) , non equivalenti topologicamente, che tra una sfera e un cubo, non equivalenti in geometria euclidea ma topologicamente equivalenti (FIGURA 1). Le equivalenze e le differenze fra oggetti topologici potrebbero essere percepite dalla mente umana a un livello tattile prima che visivo.
Gli oggetti topologici si dicono equivalenti, omeomorfi, quando condividono le stesse proprietà topologiche (dette invarianti). È possibile osservare tali proprietà sia dal punto di vista intrinseco alle figure che da quello estrinseco. Non volendo qui trattare di problematiche specifiche del campo matematico, ci limiteremo a fornire un’indicazione su cosa si intenda per omeomorfismo, osservando gli oggetti topologici dall’esterno. Un cubo e una sfera di qualsivoglia dimensione sono omeomorfi, nel senso che possono essere deformati l'uno nell'altro, in entrambi i sensi, comprimendo, piegando, allungando, ma senza ricorrere a operazioni di taglio o incollaggio, possono cioè essere trasformati l’uno nell’altro per deformazione continua. Una sfera è quindi omeomorfa non solo a un cubo (FIGURA 1), ma anche a un parallelepipedo, a una piramide, o a un oggetto regolare o irregolare di qualunque forma e dimensioni. Una sfera non è invece omeomorfa a un toro (FIGURA 2) perché la sfera e il toro hanno un diverso rapporto con lo spazio. La sfera, come gli oggetti ad essa omeomorfi, ha lo spazio intorno a sé, mentre nel toro lo spazio si trova anche all'interno dell'oggetto. Il buco nel toro non può essere eliminato per deformazione continua, vale a dire senza un'operazione di incollaggio, come la sfera non può essere trasformata in toro senza operare un taglio al suo interno. Analogamente sono omeomorfi al toro gli oggetti che hanno lo stesso duplice rapporto con lo spazio, come la tazza della FIGURA 3. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
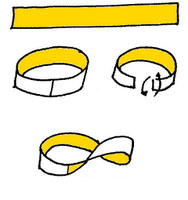
NASTRO DI MŒBIUS
Il nastro di Mœbius è una
superficie
non orientabile. Lo si può costruire per incollaggio da un
rettangolo (FIGURA
4). Se si passa una matita
longitudinalmente sul nastro senza mai staccarla
dalla superficie, si torna sulla riga già
tracciata: il nastro di Mœbius non ha un sopra e un sotto,
a differenza del rettangolo di partenza. Questa figura topologica,
esercita una
particolare attrazione, e ricorre come simbolo e come
oggetto ornamentale e artistico (FIGURE 5 e 6).
Il rettangolo e il nastro di Mœbius possono essere fatti dello stesso materiale, avere lo stesso peso, ma l'uno si trasforma nell'altro solo con operazioni di incollaggio e taglio.
Il nastro di Mœbius può essere usato come una rappresentazione geometrica dell'impossibilità di distinguere fra interno ed esterno. Si può pensare a una percezione che pur derivando da una variazione nel nostro corpo può essere confusa con la percezione derivante da un evento esterno. Se la nostra temperatura sale per un'influenza di cui ancora non siamo consapevoli, ci capita di andare a vedere se si spento l'impianto di riscaldamento, fino a che non ci rendiamo conto del nostro stato febbrile. Oppure ci può capitare, in una serata tra amici, di cominciare a sbadigliare e di far fatica a tenere gli occhi aperti. Possiamo chiederci come mai abbiamo tanto sonno, per poi scoprire che la serata è per noi noiosa, e che ci dispiaceva ammetterlo. LINK: Lungo il nastro di Mœbius: formiche, Bach, versi oulipiani e Novella dello stento |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.3. PSICOANALISI E GEOMETRIA QUALITATIVA Per la sua natura qualitativa questa geometria non euclidea può essere preziosa per lo psicoanalista che consideri importante formalizzare elementi e vicende della realtà psichica. Rimandiamo per un approfondimento all'interesse di Jacques Lacan per la topologia, e ai lavori di René Thom, volti anche a proporre strumenti vantaggiosi alle discipline che tendono alla scienza. La relazione fra psicoanalisi e scienza è rara, appassionante e spesso velata di mistero. Un breve esempio si può leggere nell'incontro con Lacan riportato da Thom, che ricorda come durante una cena vennero a parlare del matema: [J]e ne sais pas
très
bien ce que c'était que le 'mathème'!... Et lui n'a
pratiquement rien dit. A la fin du repas, j'ai utilisé une
formule qui l'a fait
réagir. Je lui ai dit: "Ce qui limite le vrai, ce n'est pas le
faux, c'est
l'insignifiant". Il a alor pris un'air songeur et il a dit: "Cela me
retient, cela me retient." Voilà:
j'avais "retenu" le Maître... (Predire
n'est pas epliquer. René Thom, à la question par
Emile Noel. Paris: Eshel 1991;
p.
132)
Certo è che il riferimento della psicoanalisi alla scienza è ricorrente in Freud, che concludeva così la Lezione 35, Introduzione alla psicoanalisi. (1932, Nuova serie di lezioni): Signore
e signori, consentitemi, per concludere, di riassumere quanto ebbi a
dire sulla relazione che la psicoanalisi ha con il problema della
"visione del mondo". La psicoanalisi, a mio parere, è incapace
di
crearsi una sua particolare Weltanschauung. Essa non ne ha bisogno,
è
parte della scienza e può dunque aderire alla Weltanschauung
scientifica. Questa, tuttavia, quasi non merita tale nome altisonante,
perché non abbraccia ogni cosa, è troppo frammentaria,
non ha alcuna pretesa di essere un tutto in sé compiuto e di
costituire un sistema. Il pensiero scientifico è ancora molto
giovane, e di moltissimi grandi problemi non è ancora potuto
venire a capo. Una visione del mondo eretta sulla scienza ha, tranne
l’accento posto sul mondo esterno reale, tratti essenzialmente
negativi, come quello di sottomettersi soltanto alla verità, nel
rifiuto di ogni illusione. Chi fra noi mortali è insoddisfatto
di questa situazione, chi pretende qualcosa di più per trovare
una momentanea consolazione, cerchi questo qualcosa dove pensa di
poterlo trovare. Noi non ce ne adonteremo: non possiamo aiutarlo, ma
nemmeno, per riguardo a lui, cambiare le nostre idee”. (OSF,
11; p. 284)
Freud non conosceva la rivoluzione epistemica nelle scienze dure,
anzitutto nella matematica, e restò sempre legato a una
concezione positivistica ottocentesca. Questo non gli ha impedito di
costruire una teoria e una pratica di lavoro con la realtà
psichica che è altrettanto rivoluzionaria rispetto ai modelli
classici della mente. Si può ipotizzare che la geometria topologica sia in qualche modo una geometria del vivente, mediante la quale si può tentare una formalizzazione della realtà psichica come insieme di processi che possono essere colti solo nella loro mobilità. Il dominio millenario della geometria euclidea, con le sue forme rigide, stabili come le statue, vale per una psiche identificata con i processi coscienti, prepsicoanalitica. I modelli deterministici della nostra mente, della nostra psiche, della nostra anima, appartengono alla storia, come l'unicità della geometria euclidea. Il decentramento del soggetto che la psicoanalisi postula come condizione per una cura di sé, esige che si tolleri la caduta dell'illusione di esercitare, ora o in futuro, o che si sia esercitata in passato, una totale padronanza sugli oggetti interni non meno che su quelli del mondo esterno. interessarsi alla topologia comporta la rinuncia al sistema di certezze che corrisponde alla concezione geometrica classica. Lo stile della psicoanalisi, nella ricerca come nel lavoro clinico, ha significative analogie con lo stile di ricerca e teorizzazione delle scienze del XX secolo, la matematica, la fisica, la biologia. La perdita della supremazia assoluta della vista nella geometria topologica può essere accostata al privilegio dato all'ascolto da Freud. Viene indebolita una posizione idealmente connessa al dio onniveggente del monoteismo, che nella pittura cristiana è spesso rappresentato come un occhio iscritto in un triangolo. Il nuovo linguaggio geometrico è al cuore di vari ambiti scientifici, sia in senso teorico che nelle applicazioni, e stimola riflessioni che portano lontano. L'espressione di questa sua fecondità trova ostacolo nella difficile rinuncia che esige da ogni ricercatore, perché destituisce radicalmente l'illusione di padroneggiamento in ogni campo di indagine. "La ragione dell'efficacia di questa invasione e colonizzazione di ambiti lontani da parte del linguaggio geometrico (sintetizzata in tutt'altro contesto nella frase di R.Thom "Capire è geometrizzare") affonda forse le sue radici nel funzionamento stesso della mente umana." (Luca Migliorini, La Geometria oggi, 2009 © Treccani XXI Secolo) La geometria topologica è feconda di ipotesi teoriche di grande respiro, già espresse da René Thom e Alexander Grothendieck, preziose per la psicoanalisi, che nasce come parte in causa della rivoluzione epistemica del Novecento. Il valore della nostra applicazione delle trecce topologiche al racconto fiabesco è forse dubbio, certo modesto. Lo presentiamo perché consideriamo valido il tentativo di applicare alle fiabe un oggetto geometrico come le trecce di Artin, che per il loro carattere qualitativo corrispondono alla natura dinamica delle fiabe e dei fenomeni della realtà psichica che esse significano. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. INTRECCI Sole eravamo e sanza alcun sospetto, le autrici di questa pagina, il 25 settembre 2009, all'Istituto Gramsci Toscano di Firenze, a seguire un ciclo di seminari sulla matematica. Era la quarta lezione di Luca Migliorini, Università di Bologna, il cui seminario si intitolava: La topologia: per una matematica tattile. Eravamo sole, nel senso che, nonostante la qualità della proposta e del docente, i presenti erano incredibilmente pochi, e sanza alcun sospetto perché non immaginavamo che il nostro docente avrebbe introdotto le trecce di Artin, di cui ignoravamo l'esistenza, come l'oggetto più narrativo della topologia. Da allora a oggi, ininterrottamente, abbiamo lavorato una volta alla settimana, per un dopocena che sconfina in direzione dell'alba, a costruire trecce per rappresentare fiabe. Pur facendo un uso matematicamente molto limitato delle trecce di Artin, senza la disponibilità di Luca Migliorini il terrore di prendere cantonate matematiche ci avrebbe potuto indurre a rinunciare a questa applicazione delle trecce di Artin agli intrecci narrativi delle fiabe. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.1. EMIL ARTIN Emil Artin (Vienna 1898 – Amburgo1962) ha dato il suo contributo a numerosi campi dell'algebra e della topologia,  aprendone di nuovi, come la teoria delle classi
algebriche e le trecce. Il campo delle trecce è
stato
aperto nel 1925, come propedeutico allo studio del campo dei nodi.
aprendone di nuovi, come la teoria delle classi
algebriche e le trecce. Il campo delle trecce è
stato
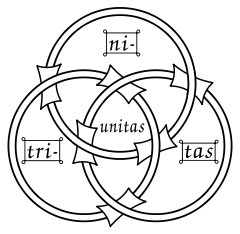
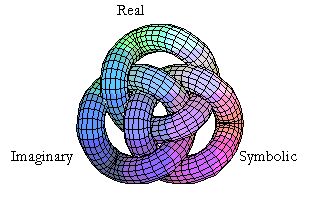
aperto nel 1925, come propedeutico allo studio del campo dei nodi. Per avere una prima idea della stretta relazione fra nodi e trecce, si osservi come da una treccia a tre capi, la comune treccia di capelli, incollando le estremità delle corde, si ottenga il nodo borromeo. Analogamente, tagliando gli anelli del nodo borromeo si torna alla stessa treccia. (FIGURA 10). Essendo necessarie operazioni di taglio e incollaggio la treccia e il nodo corrispondente non sono figure omeomorfe. FIGURA 10 Il nodo borromeo (FIGURA 11), già nello stemma della nobile famiglia milanese, è stato usato per raffigurare il dogma della Trinità (FIGURA 12). Se si taglia uno dei tre cerchi che lo compongono, gli altri due si separano: per questo è stato scelto da Jacques Lacan per rappresentare i tre registri della realtà psichica (FIGURA 13). Nel falso nodo borromeo, anch'esso usato fin dall'antichità, che è presente col nome Trinity fra i gioielli di Cartier (FIGURA 14), togliendo uno dei cerchi gli altri due restano intrecciati.
Tornando alle trecce di Artin, prima di passare alla presentazione di questo oggetto, limitata a quanto serve a capire la loro applicazione alle fiabe, bisogna ricordare che il campo delle trecce riveste un'importanza sempre crescente, oltre che in matematica, anche in altri ambiti, come la fisica e la biologia, dove si contano numerose applicazioni. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
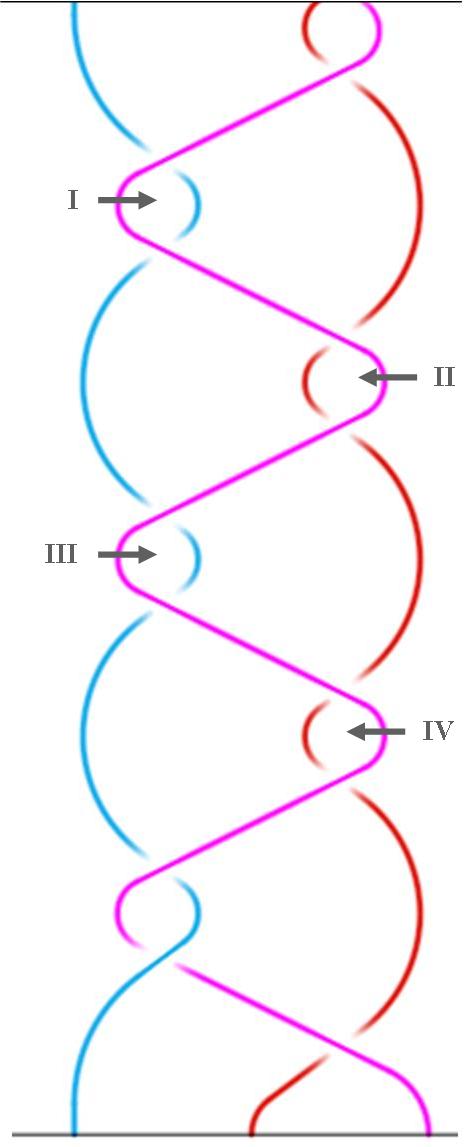
2.2. TRECCE NEL TEMPO Una treccia topologica è un oggetto tridimensionale, costituito da un certo numero di corde, denominate curve, tre nella FIGURA 10, che hanno inizio e termine su due rette parallele, che nella stessa figura non sono disegnate. La distanza fra le rette può variare illimitatamente, come la distanza fra le curve sulle rette. Le curve possono essere pensate come corde fatte di un materiale illimitatamente estensibile e contraibile, e possono fluttuare nello spazio, senza fondersi l'una con l'altra e senza intersecarsi. Le trecce hanno un orientamento nello spazio: le due parallele che le delimitano sono orientate da sinistra verso destra, mentre gli incroci che le curve formano fra loro, senza fondersi o intersecarsi, proprio come i capelli di una treccia, procedono dalla parallela di origine verso la parallela di chiusura, e da sinistra verso destra. L'orientamento irreversibile delle rette e degli incroci rende la trecce adatte a rappresentare un racconto, nel quale gli eventi si succedono nel tempo, irreversibilmente. Si pensi a un incantesimo, come quello che fa addormentare Rosaspina, o fa nascere un principe in forma di porco: c'è sempre un incantesimo di segno opposto che consente di svegliare la principessa, o di restituire al principe Porco la sua forma umana. Ma fra la maledizione e la liberazione c'è una successione temporale irreversibile, e ci sono eventi di varia natura, movimenti e incontri o scontri fra gli attanti, senza i quali la Bella continuerebbe a dormire e il principe a grugnire. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. FORMALIZZAZIONI I tentativi di formalizzazione delle fiabe iniziano con l'opera pionieristica di Marian R. E. Cox, Cinderella: Three Hundred and Forty-five Versions (London, 1892), hanno il loro momento più fecondo con Morfologia della fiaba di Vladimir J. Propp (Leningrad 1928), e sono determinanti nella raccolta e nella classificazione di tutti i motivi fiabeschi da parte della scuola finlandese, dalla quale si origina l'opera monumentale di Antti A. Aarne e Stith Thompson, The Types of the Folktale: A Classification and Bibliography. (Helsinki 1961). Tradotta e diffusa in Occidente più di vent'anni dopo la pubblicazione in Russia, la Morfologia di Propp ha esercitato una influenza determinante sullo strutturalismo francese, e quindi, indirettamente, sulla teoria di Jacques Lacan (vedi: Dmitry Olschansky, 2008, The Birth of Structuralism from the Analysis of Fairy-Tales; consultato il 22 giugno 2011). Il fatto che la formalizzazione delle fiabe di V. Propp abbia avuto effetti fecondi di vastissima portata non è estraneo alla natura delle fiabe stesse: fra tutte le forme narrative sono quelle dotate del massimo di stabilità e del massimo grado di flessibilità. Sono le storie più universali per la loro diffusione nel tempo e nello spazio, e per la massiccia presenza dei loro motivi nell'immaginario, in particolare nei film contemporanei che riuniscono un pubblico mondiale di bambini e adulti, come Avatar di J. Cameron (USA 2009). Allo stesso modo le fiabe venivano raccontate a veglia nell'aia d'estate o nella stalla d'inverno, a un pubblico che comprendeva bambini, adulti, vecchi. Le fiabe rappresentano la realtà psichica, e per questo seguono le leggi che Freud ha descritto per i sogni notturni (vedi il Capitolo VII dell'Interpretazione dei sogni [1899]). Molto più dei sogni notturni le fiabe sono governate dal criterio di rappresentabilità, che conferisce loro una particolare coerenza narrativa: sono fruibili da un pubblico quasi illimitato, senza confini di età e cultura, mentre i sogni notturni hanno un carattere privato, e spesso risultano incomprensibili per il sognatore stesso. Per la sua coerenza narrativa la fiaba fa parte dell'insieme dei racconti che comprende la novella, la leggenda, i miti, i romanzi di fantascienza o realistici. Per il suo rapporto con la realtà psichica la fiaba è oggetto privilegiato dell'indagine psicoanalitica. Per quanto le sue interpretazioni delle fiabe appaiano datate, bisogna riconoscere che si deve a Bruno Bettelheim la scoperta del valore della fiaba nell'educazione e nella cura di bambini problematici (Vedi: B. Bettelheim, The Uses of Enchantment. The meaning and Importance of Fairy-tales, 1976; vedi anche La fiaba come rappresentazione eidopoietica, in A. Gasparini, Aladino e la lampada meravigliosa. Viaggio psicoanalitico; Milano: FrancoAngeli 1993). Senza mai dimenticare che la fiaba è qualcosa di unitario, affascinante proprio per la significazione della realtà psichica unita a un'espressione poeticamente felice, possiamo immaginarla come un Giano bifronte, con una faccia rivolta all'inconscio e una rivolta alla coscienza. Qualunque interpretazione che si limiti a una delle due facce sarà parziale, non potendo cogliere il carattere specifico della fiaba, che è la ragione prima della sua efficacia comunicativa come della sua potenza nel lavoro educativo e terapeutico. Lo psicoanalista che fornito dei suoi strumenti interpretativi analizzi una fiaba senza tener conto del suo valore poetico, della lingua in cui si esprime, della cultura nella quale si racconta, potrà fornire un'interpretazione efficace, che però suonerà arbitraria e inaccettabile per gli studiosi estranei al campo della psicoanalisi. Si può interpretare una fiaba in modo convincente utilizzando qualunque teoria psicoanalitica, correndo il rischio di tradurre attanti e vicende della fiaba con i corrispondenti elementi della teoria di riferimento (vedi, di A. Gasparini, Se le metafore giocano, 2010). Dall'altra parte, il mitologo o il critico letterario che studi la fiaba senza tener conto del suo volto rivolto verso la realtà psichica, ignorando nel racconto la presenza delle leggi del sogno, non potrà dar conto della particolare potenza della fiaba stessa. Le formalizzazioni finora proposte corrispondono a modelli lineari - formule - o bidimensionali - tabelle - che appiattiscono la fiaba non potendo cogliere la terza dimensione, la profondità, il gioco prospettico fra eventi e attanti, né la quarta dimensione, il tempo, nel quale si immergono eventi e attanti per procedere, cammina e cammina, da una situazione di rischio mortale a un finale felice. Le trecce di Artin offrono una possibilità di procedere tenendo conto della fecondità e dei limiti di queste interpretazioni. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.1. TRECCE DI CENERENTOLA. RAPPRESENTAZIONE GEOMETRICA In una treccia di ordine n (n sta per un numero ordinale intero, 7 nel caso della FIGURA 15) L1 ed L2 sono rette parallele orientate da sinistra verso destra - nello stesso senso indicato nella figura dalle frecce. Se P1, P2 ... P7 sono punti su L1, e Q1, Q2 ... Q7 punti su L2, congiungiamo ciascun punto P a ciascun punto Q con altrettante curve, orientate da L1 a L2., nella nostra figura dall'alto verso il basso. 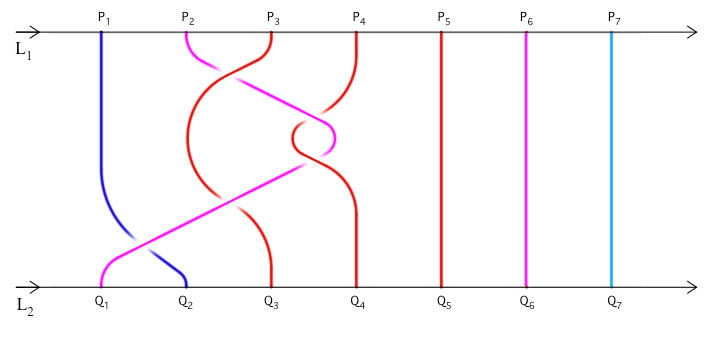 FIGURA
15
La FIGURA 15
è la proiezione bidimensionale di un
oggetto tridimensionale, nella quale gli incroci sono rappresentati
interrompendo
la curva che passa dietro a quella con la quale si incrocia, ed
è la prima delle quattro trecce con le quali si è
formalizzata La gatta
Cennerentola
(Basile, 1634).Ogni curva rappresenta un attante della fiaba, ogni incrocio un'interazione fra attanti. Si sono distinti quattro tipi di attanti colorando le corrispondenti curve: blu, attante paterno;
rosso, attante materno; celeste, attante filiale maschile; rosa, attante filiale femminile. Le trecce che formalizzano La gatta Cennerentola sono di ordine 7, nel senso che i personaggi della fiaba sono rappresentati da 7 curve. Nella prima treccia (FIGURA 15) gli attanti, da sinistra a destra, sono i seguenti: 1. il padre di Cenerentola, attante paterno (P1-Q2); 2. Cenerentola, attante filiale femminile protagonista, (P2-Q1); 3. la prima matrigna, attante materno, già presente all'inizio della fiaba (P3-Q3); 4. la maestra di cucito, attante materno, che nella seconda treccia diventerà la seconda matrigna di Cenerentola (P4-Q4); 5. la fata, attante materno, che si presenterà nella fiaba in tre forme connesse fra loro, come una colomba parlante, come la Fata Colomba e come fata del dattero, con funzione materna protettiva e donatrice (P5-Q5); 6. le sorellastre, attanti filiali femminili, che agiscono all'unisono e per questo sono rappresentate da una sola curva (P6-Q6); 7. il re, attante filiale maschile, che innamorandosi di Cenerentola ha la stessa funzione del principe in altre versioni della favola (P7-Q7). In questa prima treccia le curve corrispondenti alla fata, alle sorellastre e al regale pretendente di Cenerentola non si intrecciano fra loro né con le altre curve: sono presenti nella fiaba intesa come insieme compiuto, ma interagiscono in parti della fiaba formalizzate dalle successive trecce. Analogamente la prima matrigna, che muore nel penultimo incrocio di questa prima treccia, e non tornerà più in vita, come può capitare in altre fiabe a qualche attante, sarà rappresentata nelle trecce successive da una curva senza incroci. Le parallele L1 ed L2 rappresentano l'inizio e la fine della fiaba o, come in questo caso, di una sua parte, e restano fisse come la pagina bianca che precede e quella che segue il racconto. Limiti geometrici della treccia, rappresentano i limiti della storia. Le curve, che formalizzano gli attanti, vanno immaginate, analogamente a ogni oggetto topologico, come fatte di un materiale elastico, e per questo estensibili, flessibili e contraibili illimitatamente. La consistenza di questo materiale che le compone non permette loro di intersecarsi né di fondersi: questo significherebbe operare tagli - per far passare una curva dentro l'altra - o incollaggi - per unirne due. Analogamente due curve non avranno né la stessa origine né la stessa fine. Come due persone, incontrandosi, in guerra o in amore, sembrano fondersi ma restano sempre distinte, così le nostre curve formano incroci, vale a dire cambiamenti di posizione nella sequenza delle curve da sinistra a destra, senza mai confondersi l'una con l'altra. Liberamente fluttuanti nello spazio, le curve non possono mai invertire la direzione da L1 a L2:, che nella nostra treccia significherebbe risalire. Si formalizza con la treccia solo la fabula, ovvero la sequenza temporale degli eventi narrati, senza rappresentare quanto viene narrato per analessi (flash-back) o per prolessi (flash-forward), indipendentemente dall'importanza degli eventi così presentati. Per eventi si intendono qui esclusivamente le interazioni fra attanti, rappresentate come incroci fra curve nella treccia. Nel linguaggio di Artin gli incroci vengono espressi algebricamente con la lettera greca s, e si chiamano generatori. Nelle fiabe come trecce ogni generatore, determinando un cambiamento di posto dell'attante, rende possibile una relazione con un altro attante, rappresentato dalla curva che si viene a trovare alla sua destra dopo l'incrocio. Dalla prima treccia de La gatta Cennerentola (FIGURA 15), traiamo la treccia particolare che rappresenta i primi quattro attanti, da sinistra a destra, con i loro 5 incroci (FIGURA 16). Le didascalie che riportiamo accanto a questa figura sono le stesse che si possono vedere nella pagina che contiene il già citato schema topologico dell'intera fiaba, costituito da quattro trecce (La gatta Cennerentola). Ogni didascalia è preceduta da due numeri, il primo dei quali indica la treccia (1 in questo caso, perché è la prima treccia della Gatta Cennerentola), il secondo il generatore o incrocio della treccia (1, 2, 3, 4, 5 in questo caso).
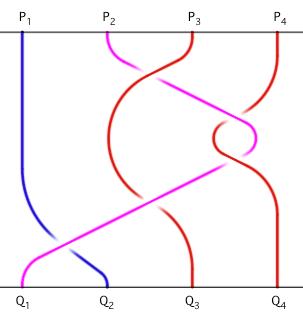
In termini matematici gli incroci fra curve si chiamano generatori, termine che abbiamo già introdotto. Suggestivamente, nella nostra applicazione, possiamo traslare il significato tecnico del termine algebrico (che fa riferimento alla teoria dei gruppi) nel significato del linguaggio naturale, nel quale generatore rimanda al concetto di far nascere, far sorgere: in questo senso, nella fiaba come treccia, ogni incrocio genera la possibilità di un incrocio fra attanti prima impossibile. Solo quando la curva di Cenerentola si è intrecciata con la curva della prima matrigna (1.1; s2¯¹), rappresentando il rapporto di vessazione che caratterizza questa e quasi tutte le versioni di Cenerentola, può intrecciarsi con la curva della maestra di cucito, con la quale Cenerentola va a lamentarsi della matrigna (1.2; s3). Cenerentola si trova ora a destra della maestra di cucito, e soltanto formando un nuovo incrocio con questa tornerà accanto alla curva della prima matrigna, con la quale si incrocerà eseguendo il piano proposto dalla maestra di cucito, ovvero facendole cadere sul collo il coperchio di un cassone e uccidendola (1.4, s2¯¹). Eliminata la prima matrigna, Cenerentola avrà alla sua sinistra la curva del padre, e formerà con questo il quinto e ultimo incrocio della prima treccia, convincendolo a sposare la maestra di cucito, che dovrebbe accontentarla in tutto e per tutto (1.5; s1¯¹). Ciascuna curva può incrociarsi con la curva che si trova alla sua destra in due modi, passandole davanti o dietro. Nella rappresentazione geometrica bidimensionale si indica questa differenza interrompendo brevemente la curva che passa dietro in ogni incrocio, avvertendo che nessuna curva si interrompe nello spazio tridimensionale. Nell'espressione algebrica si indica con l'esponente negativo (es.: 1.1; s2¯¹) il generatore nel quale la curva di sinistra (in questo caso Cenerentola) passa dietro a quella che si trova alla sua destra (in questo caso la prima matrigna). Si indica analogamente con l'esponente positivo, che si omette (es.: 1.2; s3), il generatore che rappresenta un intreccio in cui una curva (ancora Cenerentola) si incrocia con la curva alla sua destra passandole davanti (in questo caso con la maestra di cucito, futura seconda matrigna). Il numero in pedice accanto a ciascun s indica il numero d'ordine del generatore, senza alcun riferimento alla posizione iniziale delle curve che si incrociano. Il numero dei generatori è pari al numero d'ordine della treccia, dato dal numero delle sue curve, meno uno: nella nostra treccia (FIGURA 16) il numero d'ordine della treccia è 4: si hanno 4 curve e 4 - 1 = 3 generatori. Dato che gli incroci sono formati dal movimento di una curva da sinistra verso destra, la curva che si trova all'esterno a destra non potrà formare alcun incrocio, non avendo un'altra curva alla sua destra. Nel nostro caso non potranno, ad esempio, formare incroci, muovendosi da sinistra a destra, la maestra di cucito nella posizione iniziale, né Cenerentola dopo essersi incrociata con lei. Se si torna alla FIGURA 15, nella quale sono formalizzati anche gli attanti che non formano incroci in questa treccia, la treccia è di ordine 7, le curve attanti sono 7, mentre i generatori potranno essere solo 6: in questa figura sarà il re, futuro sposo di Cenerentola, a non poter formare incroci con nessuna curva, essendo l'ultimo a destra. L'osservatore attento si sarà già chiesto che significato ha nella nostra formalizzazione il passaggio delle curve davanti o dietro nei generatori. Questo è uno dei problemi più complessi che abbiamo affrontato nel nostro lavoro, al quale abbiamo dato una soluzione che ci permettesse di procedere, anche se non è molto soddisfacente. Formalizzando la fiaba abbiamo geometrizzato con la treccia l'insieme cronologicamente ordinato delle interazioni fra personaggi, cercando di abbandonare, come una zavorra, qualunque criterio moralistico, dominante in pedagogia e nel senso comune, e qualunque criterio psicologistico, inteso come una forma moderna di comune moralismo, al quale lo psicoanalista stesso talora paga un indebito tributo. Anche il simbolismo, così importante nella comprensione del valore e della ricchezza delle fiabe, è totalmente ininfluente in questa formalizzazione. Tornando al significato da attribuire al passaggio davanti o dietro di una curva sull'altra nei vari generatori, certo non ha a che fare con qualsivoglia superiorità di un attante sull'altro, né significa quindi una sottomissione dell'uno sull'altro attante. Non trovando di meglio, abbiamo scelto di rappresentare a questo proposito il contenuto manifesto della favola, decidendo che a passare davanti sarebbe stata la curva dell'attante che decide, sceglie, secondo la sua volontà, una certa interazione, distruttiva o riparatoria, nei confronti dell'attante con la cui sua curva forma il generatore. Facciamo due esempi dalla nostra prima treccia di Cenerentola, che possono essere visti nella loro rappresentazione geometrica in questa pagina sia nella FIGURA 15, sia nella FIGURA 16. Per una rappresentazione di tutta la fiaba, si rimanda nuovamente alla pagina dedicata interamente a La gatta Cennerentola. Il primo generatore (1.1; s2¯¹) formalizza l'interazione fra Cenerentola e la prima matrigna, della quale la fiaba dice che, non sopportando la figliastra, la spaventava con espressioni cattive e accigliate: ...facennole "...cere brosche, facce storte, uocchie gronnuse da farela sorreiere..." Si racconta quindi che la matrigna intendeva vessare Cenerentola, la quale, a sua volta, ne subiva la vessazione: per questo la curva della prima matrigna passa davanti alla curva di Cenerentola. Si parla di una relazione conflittuale tra madre e figlia, con un portato distruttivo sufficiente a provocare la morte di una delle due: se il contenuto manifesto attribuisce tutta la responsabilità di questa prima interazione alla prima matrigna, sappiamo che a livello inconscio l'attante protagonista si pone in posizione masochista rispetto a questa figura materna, avallandone l'aggressività. Una fiaba racconta una vicenda fra diversi attanti, ma se la leggiamo come un sogno intendiamo questi attanti come parti dello stesso soggetto, che ne riconosce alcuni come propri, mentre ne attribuisce altri, che non gradisce, ad altre figure. Cenerentola non rappresenta in questo senso una particolare fanciulla, ma gli aspetti femminili del soggetto, la sua ricettività, la sua capacità di nutrire e far prosperare, di attendere in silenzio che qualcosa cresca, senza sapere cosa sarà. In questo senso appartengono al soggetto sia la distruttività della matrigna vessatrice, sia il masochismo di Cenerentola, presentato come innocente docilità. Nella versione secentesca, di cui stiamo vedendo la prima treccia, la carica distruttiva della protagonista emerge senza mezzi termini nella violenza omicida, grazie alla quale, complice la maestra di cucito, Cenerentola spera di avere una nuova figura materna che dipenderà da lei e l'accontenterà in tutto. La sua capacità di convincere il padre a sposare la sua maestra di cucito significa la sua posizione incestuosa di compagna ideale del padre, che sembra pronto a soddisfare ogni suo desiderio. Nel secondo generatore la curva di Cenerentola passa sopra a quella della maestra di cucito (1.2, s3), perché è per iniziativa sua propria che Cenerentola si lamenta con lei, mentre è la curva della maestra di cucito a passare sopra a quella di Cenerentola nel terzo generatore, quando la maestra di cucito le suggerisce il modo di levare di mezzo definitivamente la prima matrigna (1.3, s3). Nelle trecce di Artin la curva di sinistra si muove sempre verso destra, mentre nella fiaba come treccia si ha l'impressione che Cenerentola per così dire torni indietro, dalla maestra di cucito alla prima matrigna, per ucciderla (1.4, s2¯¹), e poi al padre, per convincerlo a sposare la maestra di cucito (1.5, s1¯¹). L'espressione algoritmica di questa treccia resta in ogni caso corrispondente alla notazione di Artin. Nessuna formalizzazione sensata, complessa a piacere, tende a esaurire il senso di una fiaba, come nessuna teoria biologica può esaurire il senso della vita. La funzione di una formalizzazione non è ermeneutica, non tende a dire cosa significhi una fiaba, ma geometrizzante. Essa aspira a riconoscere varianti e costanti nelle fiabe, che permettano di riconoscere il rapporto fra versioni distinte della stessa fiaba, e tra fiabe diverse, che posso avere uno o più motivi in comune. Una formalizzazione sarà accettabile se mostrerà di essere utile in questo senso, consentendo di individuare quel che fa di versioni anche molto diverse una stessa fiaba, tanto che ascoltandola è facile riconoscere che si tratta di Cenerentola. Ipotizziamo a questo punto che versioni diverse della stessa fiaba abbiano al loro interno una treccia omeomorfa che le caratterizza. Nel caso delle trecce parliamo di omeomorfismo quando due trecce possono trasformarsi l'una nell'altra con movimenti delle loro curve che non implichino alcun taglio né alcun incollaggio. In questo senso abbiamo osservato, e ne mostreremo fra poco un esempio, come motivi fiabeschi apparentemente diversi si rivelino omeomorfi con questa formalizzazione, mentre motivi fiabeschi apparentemente simili siano irriducibili l'uno all'altro per deformazione continua delle loro curve. I risultati della nostra ricerca sono ancora modesti, sufficienti però a formulare l'ipotesi appena enunciata, che delineeremo meglio con un esempio. Prima di farlo dobbiamo dar conto di altri due aspetti nella nostra formalizzazione, il primo riguardante la successione degli attanti sulla retta L1, che rappresenta l'inizio della fiaba o di una sua parte, il secondo riguardante la divisione della fiaba in due o più parti formalizzate da trecce distinte. Come nella scelta del criterio per far passare una curva sopra o sotto l'altra curva in ogni generatore, e in misura ancora maggiore, è stato il racconto a farci adottare e quasi a imporci un metodo sia per disporre le curve degli attanti su L1 da sinistra a destra, sia per determinare il numero di trecce necessarie per formalizzare una fiaba. La disposizione delle curve, corrispondenti agli attanti che interagiscono fra loro in una certa treccia, è determinata dalla necessità di rappresentare in ordine cronologico le loro relazioni; i generatori si troveranno nella treccia ordinati analogamente da L1 a L2 . Riprendendo la FIGURA 16 osserviamo che il primo generatore è formato dalle curve di Cenerentola e della prima matrigna, che iniziano rispettivamente in P2 e P3. Se la curva della prima matrigna si originasse in P2 e quella di Cenerentola in P3, dopo il primo generatore la curva di Cenerentola si troverebbe a sinistra di quella della prima matrigna e a destra di quella del padre: non sarebbe dunque possibile formalizzare la successiva interazione narrata dalla fiaba, vale a dire fra Cenerentola e la maestra di cucito. Quanto detto può essere osservato per tutte le successive interazioni della treccia.
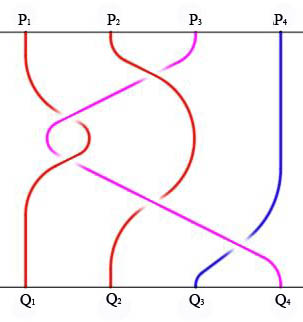
Ammesso che le interazioni fra attanti si possano rappresentare solo scegliendo una certa sequenza delle curve (padre, Cenerentola, prima matrigna, maestra di cucito), possiamo osservare che nella treccia della FIGURA 17, speculare rispetto alla FIGURA 16, l'ordine delle curve è invertito (maestra di cucito, prima matrigna, Cenerentola, padre) e i generatori si succedono nello stesso ordine. All'espressione algebrica della treccia della FIGURA 16: s2¯¹ s3 s3
s2¯¹ s1¯¹
corrisponde questa espressione della treccia della FIGURA 17: s2 s1¯¹ s1¯¹
s2 s3
.nella quale i segni dei generatori sono invertiti. In entrambi i casi le curve degli attanti passano davanti o dietro l'una all'altra nello stesso modo. Si può osservare che la fata, le sorellastre e il principe, non rappresentati per comodità nelle FIGURE 16 e 17, sono invece presenti nella FIGURA 15, anche se non prendono ancora parte attiva alla storia. Analogamente, nelle trecce successive de La gatta Cennerentola, sarà presente la curva rossa corrispondente alla prima matrigna, che viene uccisa nel primo movimento, e non torna più in vita, come accade talora nelle fiabe. Per analogia si può pensare agli attori di un'opera teatrale che sono sempre presenti anche se restano dietro le quinte, prima di entrare in scena, o dopo aver esaurito la loro parte. L'ultimo punto di questa introduzione delle Favole come trecce, riguarda il fatto che una fiaba, come quella de La gatta Cennerentola, che può essere considerata come la capostipite documentata di tutte le Cenerentole successive, sia formalizzata da quattro trecce. Per quale motivo non è sufficiente una treccia unica per rappresentare tutte le interazione fra attanti, ovvero i generatori della treccia stessa? La risposta è la stessa che abbiamo proposto per la questione precedente, relativa all'ordine delle curve su L1: una treccia si chiude quando le posizioni occupate dagli attanti a un certo punto della formalizzazione impediscono di continuare a rappresentare le successive interazioni del racconto. A questo proposito, per quanto abbiamo cercato il modo più semplice per formalizzare le fiabe come trecce, siamo certe che ogni nostra treccia potrebbe essere migliorata: è quello che abbiamo fatto nell'arco di tutti i nostri incontri di ricerca, e avremmo potuto continuare se non ci fosse parso necessario presentare i nostri primi risultati. Il numero di trecce che costituiscono lo schema topologico della fiaba, rappresentato geometricamente e algebricamente, è il numero minimo delle trecce necessarie per formalizzare l'insieme delle relazioni fra attanti narrate nella fiaba, cronologicamente ordinate. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.2. TRECCE DI CENERENTOLA. ESPRESSIONE ALGEBRICA Abbiamo introdotto la prima treccia de La gatta Cennerentola, descrivendone sia la figura sia l'algoritmo. Abbiamo chiamato schema topologico l'insieme delle trecce che formalizza una favola e che consta, nelle favole da noi finora formalizzate, di un numero di trecce che va da 1 a 7. Nel caso de La gatta Cennerentola le trecce sono 4, per le quali si rimanda ancora una volta alla pagina relativa. Abbiamo applicato a questi algoritmi la proprietà associativa, per ottenere algoritmi più semplici, che chiameremo paradigma della fiaba. Il numero delle trecce e degli algoritmi ovviamente non varia passando dallo schema topologico al paradigma della stessa fiaba (4 nel caso de La gatta Cennerentola). Come il paradigma di un verbo dà conto della sua coniugazione, così il paradigma di una fiaba dà conto delle relazioni trasformative fra gli attanti. È altresì vero che come il paradigma di un verbo non include la varietà delle forme verbali che si possono incontrare in un discorso, il paradigma della fiaba non include la varietà dei generatori che formalizzano tutti gli intrecci fra attanti di un certo racconto.
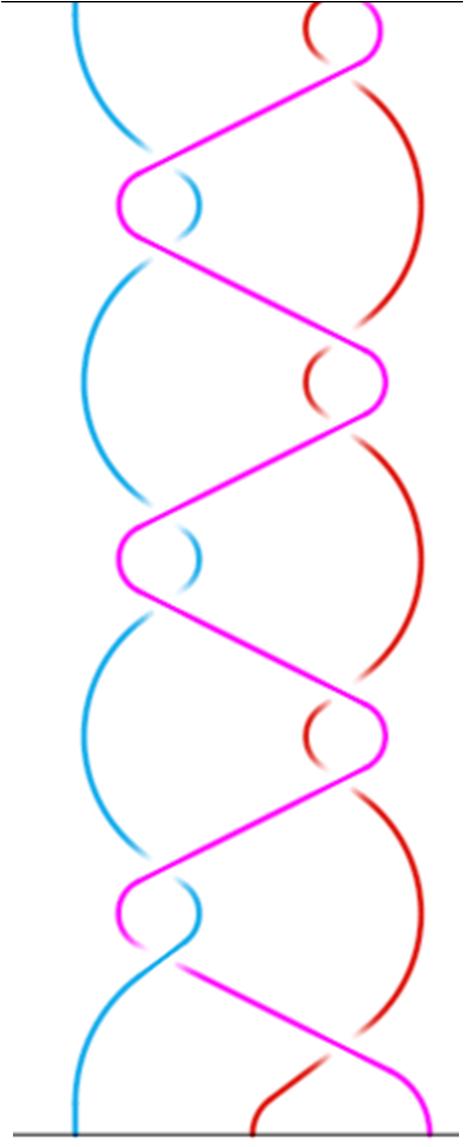
Per spiegare cosa significa il paradigma di una treccia, come si ottiene, e quali potenzialità abbia nello studio delle fiabe, delle loro varianti e delle loro costanti, procediamo con un esempio, traendolo dalla treccia 3 de La gatta Cennerentola. Avremo una nuova treccia, isolata dalla treccia 3 completa, nella FIGURA 18. Il numero d'ordine delle didascalie e il numero in pedice dei generatori corrisponde a quello della treccia 3 completa.
La gatta
Cennerentola viene magicamente vestita dalla fata, si reca alla
passeggiata dove si trova il re, e il re se ne innamora. Cenerentola
fugge, inutilmente inseguita per ordine del re, e si fa spogliare dalla
fata del dattero per tornare accanto al focolare come se non se ne
fosse mai allontanata. L'intero movimento, costituito da 4 generatori (s2¯¹
s1¯¹
s1
s2) si ripete una seconda volta. La terza
volta i generatori che si ripetono sono il primo, il secondo e il
quarto: il terzo generatore è formato dalle stesse due curve,
corrispondenti a Cenerentola e al suo regale pretendente, ma questa
volta non è la curva di Cenerentola a passare davanti al re,
bensì quella del re a passare davanti a quella di Cenerentola.
Vale a dire che nei primi due casi l'intenzione manifesta di
Cenerentola rispetto al re costruiva una relazione di fuga, mentre la
stessa intenzione, nel terzo caso, fallisce dato che si realizza
l'intenzione del re di raggiungere Cenerentola. Questa intenzione ha
successo perché il re, impadronendosi della scarpetta, che,
detto per inciso, è l'oggetto più famoso di tutte le
fiabe del mondo, mette fine alla ripetizione del doppio movimento di
esibizione e occultamento dell'attante protagonista. L'esultanza del re
di questa prima versione di Cenerentola esprime poeticamente
l'importanza del generatore 3.17:
Lo quale, pigliatolo ’n
mano, disse: « Se lo
pedamiento è
cossì bello, che sarrà la casa? O bello canneliero, dove
è stata la cannela che me strude! O trepete de la bella caudara,
dove volle la vita! O belle suvare attaccate a la lenza d’Ammore, co la
quale ha pescato chest’arma! Ecco, v’abbraccio e ve stregno e, si non
pozzo arrevare a la chianta, adoro le radeche, e si non pozzo avere li
capitielle, vaso le vase! Già fustevo cippo de ’no ianco pede,
mo site tagliole de ’no nigro core ; pe vui era auta ’no parmo e miezo
de chiù chi tiranneia ’sta vita, e pe vui cresce autrotanto de
docezza ’sta vita, mentre ve guardo e ve possedo ». Cossì
dicenno, chiamma lo scrivano, comanna lo trommetta e tu tu tu fa
iettare no banno: che tutte le femmene de la terra vengano a ’na
festa... (Per il testo completo e la traduzione italiana, vedi La
gatta Cennerentola)
In tutte le versioni di Cenerentola ricorrono gli intrecci che per la
versione de La gatta Cennerentola
sono rappresentati nella FIGURA 18,
con le varianti descritte nella tabella sottostante. Per ciascuna
versione si rimanda agli schemi topologici completi.
Negli schemi topologici delle quattro versioni di Cenerentola qui presentati è possibile osservare come le varianti di ciascuna favola non impediscano di riconoscere la ricorrenza di intrecci messa qui in evidenza. Torniamo all'algoritmo della treccia della FIGURA 18, già presentato: s2¯¹
s1¯¹
s1
s2
s2¯¹
s1¯¹
s1
s2 s2¯¹
s1¯¹
s1¯¹
s2
Semplifichiamo ora questo
algoritmo, nel quale figurano in sequenza tutte le interazioni fra i
tre attanti narrati dalla fiaba, ovvero fra la fata e Cenerentola, e
fra Cenerentola e il principe.
Le coppie di generatori | s1¯¹; s1 | ed | s2 s2¯¹ | si annullano essendo di segno opposto. Scompaiono così il secondo e il terzo generatore, il quarto e il quinto, il sesto e il settimo, e l'ottavo e il nono. Applicando la proprietà associativa raccogliamo il decimo e l'undicesimo generatore. Abbiamo quindi il seguente algoritmo, che sarà parte del paradigma della nostra favola: s2¯¹
s1¯²
s2
Dall'espressione algebrica passiamo ora all'osservazione della figura geometrica corrispondente. Si osservi ora la FIGURA 18 ricordando che rappresenta un oggetto tridimensionale e che le curve vanno pensate come corde fatte di un materiale che le rende illimitatamente allungabili e contraibili. Si immagini ora di sollevare con quattro movimenti le corde con le dita, in corrispondenza delle frecce e nella direzione indicata nella FIGURA 20: con un po' di pazienza si può vedere come una deformazione continua, senza tagli e senza incollaggi, dia luogo alla treccia della FIGURA 21, omeomorfa alla precedente. Ricordando che la geometria topologica è tattile prima che visiva, ci si può aiutare con quattro cordicelle opportunamente fissate su un cartoncino. Le scriventi per molti mesi hanno usato questo metodo, prima di riuscire a vedere le trecce con semplici disegni bidimensionali come quelli che qui si presentano, consumando metri e metri di cordicelle colorate.
 La treccia della FIGURA 21 è
omeomorfa alle due
precedenti, ed è, come la FIGURA 20, la
rappresentazione geometrica del seguente algoritmo, già
riportato sopra: La treccia della FIGURA 21 è
omeomorfa alle due
precedenti, ed è, come la FIGURA 20, la
rappresentazione geometrica del seguente algoritmo, già
riportato sopra:s2¯¹ s1¯² s2 Quel che è presente con evidenza in tutte le versioni di Cenerentola è il paradigma, di cui abbiamo appena dato un esempio, mentre lo schema topologico, rappresentando tutte le interazioni narrate da una particolare favola, presenta maggiori differenze. Passiamo a questo punto al contenuto della favola. Le interazioni che si eliminano semplificando l'algoritmo esteso, quello relativo allo schema topologico, passando all'algoritmo semplificato, relativo al paradigma della fiaba, riguardano, come si è già detto, due tipi di interazione di Cenerentola: quella con la fata dalla quale si spoglia e si veste, e quella col principe al quale si mostra e al quale sfugge. Abbiamo visto che nella versione di Walt Disney manca la ripetizione di questa doppia interazione: Cinderella viene vestita solo una volta dalla fata, si reca una sola volta al ballo, perde la scarpetta, e si trova vestita dei suoi stracci perché l'incantesimo finisce a mezzanotte. In Perrault si veste e si reca al ballo, e poi si trova spogliata dopo i rintocchi della mezzanotte per due volte, mentre in Basile e nei Grimm Cenerentola per tre volte si veste magicamente, e per tre volte magicamente si spoglia. Appare quindi al principe o al re per tre volte, le prime due gli sfugge senza farsi riconoscere, mentre la terza lascia dietro di sé la sua calzatura. Lo chianiello della versione di Basile, la scarpetta d'oro dei Grimm, la più celebre scarpetta di vetro o di cristallo di Perrault, preferita da Disney, è metonimicamente Cenerentola stessa, appartiene a lei sola, e sarà sufficiente a identificarla, chiamandola fuori dalla cenere del focolare dove sta nascosta (Per un'interpretazione di questo motivo, vedi: A. Gasparini, La luna nella cenere). La nostra formalizzazione non comprende gli oggetti magici, ma si può dire che gli intrecci ne rivelano l'importanza: in tutte le versioni di Cenerentola l'occultamento dell'attante protagonista, costretta a servire e  a non mostrarsi al
ballo dalla
matrigna vessatrice, non finisce quando si reca al ballo, ma quando il
suo regale pretendente si attiva catturando la scarpetta che la
rappresenta. a non mostrarsi al
ballo dalla
matrigna vessatrice, non finisce quando si reca al ballo, ma quando il
suo regale pretendente si attiva catturando la scarpetta che la
rappresenta. Cenerentola è l'attante fiabesco più famoso del mondo, e la sua scarpetta è anche più nota della lampada di Aladino. Mentre lo chianiello di Basile, come la calzatura di tante versioni popolari che qui non presentiamo, non è né piccolo né grande, ma giusto solo per il piede di lei, la scarpetta d'oro dei Grimm non può essere calzata dai piedi troppo grandi delle sorellastre, come la scarpetta di cristallo della Cenerentola di Perrault e di Walt Disney. Il successo del simbolo è comprensibile se è legato alle interazioni che le nostre trecce formalizzano: solo quando il regale pretendente ne entra in possesso la fuggitiva può essere finalmente raggiunta. La grazia di Cenerentola che volteggia nel ballo, la sua leggerezza che la rende irraggiungibile nella fuga, nella sua carrozza magica che sembra spiccare il volo per fuggire all'inseguitore in Basile, i suoi salti acrobatici per rientrare in casa, dal granaio o dal pero, per non essere raggiunta dal principe nei Grimm, sono presenti nella scarpetta di cristallo che tutti ricordano. Si può riflettere su questa calzatura: il fatto che sia di cristallo la rende assolutamente irrealistica come calzatura per ballare, e se Cenerentola corresse indossandola la romperebbe ferendosi. Così la poesia della fiaba rappresenta un sogno, una leggerezza e un'eleganza illimitate, e la loro distanza da qualunque traduzione realistica. È stato ipotizzato che questo materiale impossibile quanto poetico, derivi da un felice errore di Perrault, che scrisse verre, vetro, traducendo il termine che nella versione popolare dalla quale attinse era vaire, omofono ma di diverso significato: vaire era vaio, una morbida e preziosa pelliccia. Forse il simbolo della scarpetta, come ogni simbolo, può essere compreso solo a partire dal contesto narrativo che lo contiene. Audrey Hepburn e Fred Astaire in Funny Face (titolo italiano: Cenerentola a Parigi) Stanley Donen, USA 1957 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. GEOMETRIE DI FAVOLA Quale significato possiamo attribuire a questo punto alle ripetizioni presenti in tante versioni di Cenerentola, alle interazioni con la fata e con il principe? Perché non accade come in Disney, al quale basta un abito magico, e un'apparizione al ballo, con una sola fuga? La versione di Disney è la sola che conosciamo dove manchi la ripetizione del motivo formalizzato nella FIGURA 18. Ciò che nell'algoritmo scompare, i generatori che scompaiono con le mosse indicate nella FIGURA 19, (in matematica sono le mosse di Reidemeister) risultano da interazioni dove il movimento dipende dall'intenzione di un solo attante: è Cenerentola che chiede alla fata del dattero abiti e carrozze per andare a farsi vedere senza essere riconosciuta nella versione di Basile come nella versione dei Grimm: la sua curva passa davanti a quella dell'aiutante materna sia quando si veste sia quando si spoglia. È ancora Cenerentola a mostrarsi al re e a fuggirlo, nei due primi incontri, nelle stesse due versioni. Nessun vincolo le impone di tornare a qualche ora o di fuggire, come accade nelle più celebri versioni di Perrault e Grimm. In queste altre versioni, al contrario, è la figura materna soccorrevole, la fata madrina, a vestirla e a spogliarla, e la curva che rappresenta Cenerentola passa sotto a quella della fata. Allo stesso modo si sciolgono gli intrecci, senza che nulla sia cambiato, finché le interazioni col principe sono decise da Cenerentola, mentre la storia cambia quando la curva del principe passa sopra a quella della fuggitiva, quando il suo desiderio di ritrovarla prevale sulla fuga di lei, quando si impadronisce della sua scarpetta. Concludiamo questa introduzione osservando che ciò che cambia gli eventi è un'interazione fra attanti che non si scioglie, e questo accade quando la volontà o il desiderio di entrambi gli attanti implicati in due generatori si afferma. Forse il senso più interessante di questa formalizzazione è proprio in questo: ogni trasformazione, ogni storia che procede, implica un'incontro generato dal desiderio e dall'azione di due attanti. Le ripetizioni appaiono come preparazione di questo incontro, come nella vita: poche cose importanti accadono al primo tentativo. Ci sono fiabe, di cui presenteremo appena possibile le trecce, in cui si danno nozze regali o altre trasformazioni all'inizio della storia: in questi casi il racconto dice di come quel che si è ottenuto senza un cammino, senza dolore, senza elaborazione, si perda, e vada riconquistato. Con tutti gli intrecci che devono esser fatti, con attanti paterni e materni ostili e soccorrevoli, con sorelle e fratelli altrettanto ostili o soccorrevoli, e con attanti dell'altro sesso, che si trovano e si perdono e si ritrovano: verso un lieto fine che è tutt'altro che facile da raggiungere. Cenerentola, che si chiami gatta Cennerentola, Cendrillon, Aschenputtel o Cinderella, fugge agile e leggera, con la stessa grazia con la quale volteggia nella sala da ballo del palazzo reale. Perché fugge? perché, visto che la sua storia prevede il lieto fine, non svela subito il suo nome al suo regale pretendente, innamorato a prima vista e deciso a sposarla? perché in tutte le versioni, tranne che in quella di Disney, si fa vestire con abiti stupefacenti, per poi tornare nella cenere del focolare? Perché la matrigna e le sorellastre non devono sapere che la bellissima fanciulla di cui il principe si innamora è la stessa che siede nel canto del fuoco, sempre stracciata e sporca di cenere? Che cos'è la ripetizione, descritta da Freud come Thanatos, coazione a ripetere? Se la gatta Cennerentola avesse avuto un analista freudiano, se avesse fatto le sue sedute fra un ballo e l'altro, fra un cambio d'abito e l'altro, non sarebbe stata considerata isterica? Non le sarebbe stato chiesto per quale ragione continuava a farsi vestire e spogliare dalla fata del dattero, visto che il principe era deciso a  sposarla?
sposarla? È inutile, se non dannoso, interpretare una fiaba come se l'attante protagonista, o il suo autore, quando c'è un autore, fossero in analisi. È inutile, se non dannoso, pensare che il senso di una fiaba che ha attraversato confini di tempo e di spazio per quattro o cinque secoli, vivendo poeticamente in tutti gli angoli del mondo, senza mai dar segni di invecchiamento, agile tanto da muoversi tra comunità analfabete, circoli letterari raffinati come quello al quale apparteneva Giambattista Basile, corti sontuose come quella del Re Sole per la quale scriveva Charles Perrault, come l'industria cinematografica di Walt Disney, si possa comprendere applicando meccanicamente una teoria psicoanalitica o esercitando ermeneutiche anche raffinate. Cenerentola è una parte importante dell'immaginario mondiale. Nel 1892 Marian E. R. Cox ne aveva raccolte 345 versioni; digitando oggi Cinderella su Google appaiono 19.000.000 risultati, 2.900.000 digitando Cenerentola, 1.100.000 per Cendrillon, 888.000 per Aschenputtel. Non riportiamo il numero imponente di siti che offrono matrimoni in stile Cenerentola, con carrozza, castello per il ricevimento, bomboniere e abiti. Si trovano in commercio scarpette di Cenerentola di ogni materiale, a partire da quelle di un materiale plastico che imita il vetro o il cristallo. Avevano il nome di Cenerentola un paio di sandali tempestati di diamanti, di un valore letteralmente favoloso (FIGURA 22). FIGURA
22
Sandali di
Cenerentola
(valore 2.000.000 di dollari) indossati dalla cantante Allison Krauss nella notte degli Oscar del 2004 La treccia della FIGURA18, che con le mosse di Reidemeister indicate nella FIGURA 19 si trasforma nella treccia omeomorfa delle FIGURE 20 e 21, caratterizza tutte le versioni di Cenerentola che conosciamo, anche se al momento lo mostriamo solo nelle quattro versioni che abbiamo scelto. Ipotizziamo che Cenerentola significhi qualcosa del femminile talmente importante da dar conto dellasua funzione nell'immaginario collettivo, certo non solo infantile. Ipotizziamo quindi che la treccia delle figure sopra ricordate rappresenti questo qualcosa. La favola parla del lutto vissuto dal soggetto in seguito alla scomparsa della figura materna positiva, al posto della quale si trova una matrigna vessatoria. Parla quindi dell'oscurità dolorosa, solitaria, nella quale solo lavori domestici, di cura della casa, che rappresenta sia la madre, il corpo materno come il proprio corpo, riparano la lacerazione della perdita. Il tempo senza tempo del lutto, mai definito dalla favola, volge alla fine quando emerge il desiderio del soggetto di mostrare la propria bellezza. Perché questo desiderio si realizzi il soggetto, l'attante, Cenerentola, deve formarsi, acquisire un'identità, e l'abito significa l'identità. Questa formazione non va pensata come una somma di elementi, anche se diversi elementi sono necessari, ma come lo sbocciare di un fiore, come un processo che è del dominio della natura, nell'accezione del termine che usavano i greci, fusij, e che allo stesso tempo richiede, per così dire, le cure di un giardiniere e condizioni favorevoli di luce e calore. Torneremo successivamente su questo concetto, per il momento intendiamo osservare che esso si compie con una serie di passaggi che Cenerentola compie fra la fata e il principe. Cenerentola riceve doni meravigliosi, che la portano a mostrare la sua grazia femminile, da una fonte materna: nelle nostre quattro versioni abbiamo la fata del dattero che lei ha coltivato, l'alberello cresciuto sulla tomba della madre e annaffiato con le sue lacrime, e la fata madrina. Questa grazia femminile attiva il desiderio del principe, e le ripetizioni possono essere intese come momenti successivi che confermano e consolidano la piena fioritura di Cenerentola. La fiaba potrebbe esprimere con la ripetizione la durata nel tempo del processo, che non si dà in una sola battuta, il suo farsi, che mette in risonanza lo stesso processo in chi racconta o ascolta, legge o vede la fiaba stessa. Non si tratta forse della stessa esperienza di un movimento trasformativo in analisi? che solo dopo il suo compimento - ammesso e non concesso che qualcosa sia mai da considerare davvero compiuto nell'esperienza umana - è visibile, narrabile, raffigurabile? Ma come si potrebbe intendere questo finale felice, indice della vitalità di un percorso, senza coglierne la durata? Non ci racconta forse la fiaba che la fioritura femminile ha bisogno di due relazioni, alternate e ripetute, una con la figura materna donatrice, l'altra con la figura maschile? di due desideri, di acquisire identità dalla madre, e dal desiderio maschile che riconosce la bellezza che questa identificazione positiva, dopo tante vessazioni luttuose, presenta? Cenerentola fugge per poter tornare, appare per potersi nascondere, si occulta per splendere. Le sue scarpette di cristallo, di vaire o di verre, sono nel loro significato più vere di qualunque calzatura, perché è impossibile indossarle e perché solo indossandole si può volteggiare nel ballo a corte. Chi ama la ricchezza lussureggiante dei simboli li troverà intatti, e come più nitidi, dopo aver compreso questi intrecci. Ma solo gli incontri necessari, le relazioni fra attanti giovani e vecchi, che lasciano il trono e lo conquistano, che si allontanano dai genitori e che li ritrovano, combattendosi e amandosi, raccontano di una trama, tessono una tela, dove l'arbitrio dell'ermeneutica lascia il posto a una geometria che si muove come le curve fluttuanti nello spazio. Il desiderio di comprendere le fiabe, la ragione della loro vitalità, la fecondità del loro uso psicoanalitico nell'educazione e nella cura dei bambini, e la percezione di una loro struttura rigorosa, che è una cosa sola con la loro leggerezza poetica, è alla base di questa ricerca. In qualche modo il nostro lavoro cerca di rispondere a questa domanda di René Thom: ...[L]a geometria euclidea classica si
può considerare come una magia: al prezzo di una distorsione
minima delle apparenze, (il punto senza estensione, la retta
senza spessore...), il linguaggio puramente formale della geometria
descrive adeguatamente la realtà spaziale. In questo senso, si
potrebbe dire che la geometria è una magia che ha successo. Mi
piacerebbe enunciare la reciproca: ogni magia, nella misura in cui ha
successo, non è necessariamente una geometria? (René Thom, Stabilità strutturale e
morfogenesi. Saggio di una teoria generale dei modelli. Torino:
Einaudi 1980; p. 15, n. 4).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ringraziamenti Ringraziamo il matematico Luca Migliorini, per l'apertura culturale con la quale ci ha introdotto alle trecce e ha risposto ai nostri quesiti; gli insegnanti che hanno partecipato questo e lo scorso anno ai seminari sulla fiaba promossi dall'Assessorato all'Educazione del Comune di Firenze, per il loro interesse; Antonio Maiolino, psicanalista e direttore del Centro Paul Lemoine, Scuola di Specializzazione in Psicoterapia, Sede di Napoli, per la fiducia, gli allievi della Scuola di Specializzazione per l'attenzione e il desiderio di approfondire; Patrizia Cammunci e Antonello Luigi Armando, psicoanalisti, per l'affettuoso sostegno; Antonello Sciacchitano, psicanalista, per la critica radicale; Noemi Rossi e Stefano Gorini per la cura con la quale hanno elaborato le trecce per questo sito; i parenti e gli amici per la pazienza e la curiosità con cui ci hanno ascoltato, guardando le nostre prime trecce di cordicelle colorate. Siamo grate a tutti per
le
domande imbarazzanti e per gli
spunti critici non meno che per la generosa attenzione.
|

| icoanalisi psicanalisi fiabe
fiaba favole favola formalismo
strutturalismo morfologia geometria matematica topologia trecce
cenerentola psychoanalysis fairy tales märchen contes de fées skaszki formalism structuralism morphology geometry mathematics topology braids cinderella aschenputtel cendrillon |