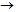|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
WHY SHOULD WE THINK OF A GEOMETRICAL STRUCTURE OF FAIRY TALES? |
Why should we think of a geometrical structure of fairy tales coming before every interpretation, why we would try to unravel the way any hermeneutic, be it ancient or contemporary, may suitably describe them? Why are fairy tales endowed with the highest degree of democracy, that makes them travel through time and space, among children and adults, among sophisticated scholars and illiterate story-tellers? What gives their patterns the chance to intertwine, to match and solve themselves, between East and West, at the court of the Sun King or the Caliph Harun ar-Rashid as well as in a souk and a farmyard? Why they may be such a helpful tool in education and terapy? Their bending to the interpretation is at the same time their indipendence from the interpretation itself, and this tells something that unites us all: can we listen to them so that we understand something about our mind, about our oneness that is also our community? The language of the science is mathematical. This research grounds on this hypothesis: to understand fairy tales, that is one of the paradigmatic expression of the individual and collective psyche, we could look for instruments in the field of topology. Who devotes himself to the complexity of the psychic reality, inaugurated by Sigmund Freud, might find in this qualitative geometry of great worth inspiration and resonance. Therefore we would formalize fairy tales by a topological object, the braids, hoping that our modest means are not an unsurmountable hindrance. Just a scientific approach has the chance to avoid the risk of any hermeneutic system, that, when successful, it comes to the same end: to explain obscura per obscuriora. Even any interpretation trying to explain everything gets an empty oversemplification: when the scholar fullfills his cage, the fairy tale already flew far away. Our formalization thinks of the transformer movement of the fairy-tale as of a il movimento trasformativo della fiaba come a set of relations between actants, structured in an irreversible temporal order. The various actants, of which we can think as schematic characters, expressive for the particular culture where a fairy-tale is written or told, correspond in a psychoanalytic key to figures belonging to the psychic reality of the person who is reading or listening. We described four kinds of actants, two for the parental characters, two for the filial characters. Every fairy tale tells the story of a main actant, male or female, however in a filial condition, who intertwines his way with parental figures, often both male and female, sometimes with other male or female filial figures, and with a filial figure of the opposite gender, if and only if at the fairy tale's there is a royal wedding. Every character is therefore inscribed in one of this four actantial typologies, depending on the function that he/she performs with relation to the main actant of the fairy tale, who, as we already said, is inscribed in the female or male filial type. We offer in this page a brief description of the intertwines that geometrize the relations among the various actants, presentig, as an example, a part of the braids formalizing one tale, the most popular in the world: Cinderella. We chose the first version of the tale, La gatta Cennerentola (Napoli 1634). We propose in this website the complete formalization of this version (Basile, 1634) and of other three significant Cinderellas (Perrault, 1697; Grimm, 1812; Disney, 1950), accessible by the home page too. These braids are provided with subtitles enabling when the mouse gets over it, and they contain the uncut version of the fairy tales. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1.
|
Topology is a geometry that
studies the properties which
define shapes and figures in space regardless their sizes. It has a
great importance in geometric and mathematical fields, and it is rich
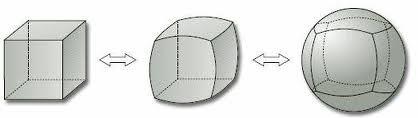
in considerations and applications for contemporary science. The difficulty encountered to understand the nature of topological objects consists in the resistance to give up the sense of mastery that measures support, privileging the view rather than the other senses. Understanding the topological objects, with their equivalences and their non-equivalences, requires that we activate a more basic perception than solving an analogous problem in Euclidean geometry: a child or a person blind from birth would distinguish the difference between a sphere and a torus (Figure 2), topologically not equivalent, more easily than between a sphere and a cube, topologically equivalent (Figure 1). The equivalences and the differences among topological objects may be perceived by the human mind in a more basic level, the first tactile than visual.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.2. UPPER IS UNDER: MŒBIUS STRIP
|
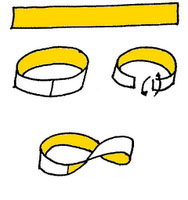
The Moebius strip is a not orientable surface. You can build it glueing a rectangle (Figure 4). If you pass a pencil lengthwise on the strip without never detaching from the surface, you will be back on the line already drawn, because this object has not a top and a bottom, unlike the rectangle you start with. The Moebius strip, like other topological objects, exerts a special attraction, and it is used as a symbol and as an ornament and artistic object (Figures 5 and 6). The rectangle and the Moebius strip can be made of the same material, have the same weight, but you will get each from the other respectively by gluing and cutting. When you consider that the rectangle has two distinct surfaces while the Moebius strip has only one you will understand immediately that they are not homeomorphic objects.
The Moebius strip
can be used as a geometric representation of the inability to
distinguish between internal and external. You can think of a
perception that comes from a change in your body and that is
indistinguishable from a perception caused by an external event. When,
for example, our temperature is rising because of a flu we are not
still aware of, it happens that we believe that the outside temperature
is lowered, until we realize our fever. It may occur that, while we are
spending the evening with friends, we start to yawn and wonder why we
nod off, before realizing
that the evening
is unexpectedly boring.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.3. PSYCHOANALYSIS AND QUALITATIVE GEOMETRY |
This geometry may for its qualitative nature be precious for a psychoanalyst who would regard to a formalization of figures and events of the psychic reality as to a main issue. For a reflection about this point, see Jacques Lacan's interest in topology, and the works by René Thom, that propose advantageous tools to disciplines leaning toward science. The relation between psychoanalysis and science is rare, fascinating and often veiled in mystery. To get a short example we can remember an exchange between Jacques Lacan and René Thom, who tells that during a dinner they came to speak about the mathema: [J]e ne sais pas
très
bien ce que c'était que le 'mathème'!... Et lui n'a
pratiquement rien dit. A la fin du repas, j'ai utilisé une
formule qui l'a fait
réagir. Je lui ai dit: "Ce qui limite le vrai, ce n'est pas le
faux, c'est
l'insignifiant". Il a alor pris un'air songeur et il a dit: "Cela me
retient, cela me retient." Voilà:
j'avais "retenu" le Maître... (Predire
n'est pas epliquer. René Thom, à la question par
Emile Noel. Paris: Eshel 1991;
p.
132)
The reference of psychoanalysis to science is however recurring in Freud, who in 1932 concluded with these words his Lesson 35 (New introductory lessons on psycho-analysis) : Ladies
and Gentlemen – Let me in conclusion sum up what I had to say about the
relation of psychoanalysis to the question of a Weltanschauung.
Psychoanalysis is not, in my opinion, in a position to create a Weltanschauung
of its own. It has no need to do so, for it is a branch of
science, and can subscribe to the scientific Weltanschauung. The
latter, however, hardly merits such a high-sounding name, for it does
not take everything into its scope, it is incomplete and it makes no
claim to being comprehensive or to constituting a system. Scientific
thought is still in its infancy; there are very many of the great
problems with which it has as yet been unable to cope. A Weltanschauung
based upon science has, apart from the emphasis it lays upon
the real world, essentially negative characteristics, such as that it
limits itself to truth and rejects illusions. Those of our fellowmen
who are dissatisfied with this state of things and who desire something
more for their momentary peace of mind may look for it where they can
find it. We shall not blame them for doing so; but we cannot help them
and cannot change our own way of thinking on their account.
(Publ. Hogarth Press, reproduced by http://www.marxists.org/;
accessed July 31th)
Freud did not know the epistemic revolution in XX century sciences,
especially in mathematics, being always related with a nineteenth
century positivistic conception. This did not stopped him to build up a
theory and a method of treatment with psychic reality that is a
revolution of the classic mind models.The topological geometry may be seen as a geometry of the living, that enables us to try a formalization of the psychic reality got as a set of events that we may catch only in their movability. The thousand-year rule of the Euclidean geometry, with its rigid figures, stable like statues, applies to a psyche identified with the conscious processes, pre-psychoanalytic. The deterministic models of our psyche, and of our nervous system, ofbelong to the history of sciences, as well as the exclusive rule of Euclidean geometry. The loss of the centrality of the ego is a condition required by psychoanalysis to take care of onself, and it asks that one stand for the fall of the illusion to wield a total mastery on one's own internal objects as well as on external ones. Topology started to develop itself when it became possible a weakening of the classic geometry, that sets figures and their measures. The psychoanalytic style of research, and its style of treatment, corresponds to the style of research and theorization that characterizes the twentieth century sciences, mathematics, physics, biology. The loss of the absolute supremacy of the eyesight in the topological geometry may be compared to the privilege granted by Freud to the listening. It is weakened a stance ideally linked to the all-seeing god of the monotheism, who is often r represented in Christian pictures by an eye inscribed in a triangle. This new geometrical language is in the core of many scientific fields, and it may sharpen fruitful reflections. The expression of this fertility is obstructed by the hard renunciation that it requires from any scholar. It demands to give up the illusory mastery of the subject that characterizes the classic culture. "La
ragione dell'efficacia di questa invasione and colonizzazione di
ambiti lontani da parte del linguaggio geometrico (sintetizzata in
tutt'altro contesto nella frase di R.Thom "Capire è
geometrizzare") affonda forse le sue radici nel funzionamento stesso
della mente umana." (Luca Migliorini, La
Geometria oggi, 2009 ©
Treccani XXI Secolo)
["The reason of the effectiveness of this invasion and colonization of distant fields by the geometric language (summarized in another context by the sentence of R.Thom "Understanding is geometrizing") may sink its roots in the same working of the human mind." Ours tr.] The topological geometry is fruitful of wide scope extensive hypotheses, already expressed by René Thom and Alexander Grothendieck, that may be precious for psychoanalysis, that was born as a part of the nineteenth century epistemic revolution. The value of our application of the topological braids topologiche to the fairy tales may be doubtful, and it is surely modest. We present it because we consider worth the try to formalize fairy-tales by a topological object. The braids of Artin have a qualitative nature that corresponds to the dynamic nature of the fairy-tales and of the events of the psychic reality that they represent. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. INTERTWINEMENTS |
Sole eravamo and sanza alcun sospetto... alone we were and without any fear, the authors of this page, Sept. 23, 2009, at Istituto Gramsci Toscano in Florence, following a series of seminars on mathematics. We were alone, in the sense that, despite the quality of the proposal and the teacher, there were incredibly few people attending to the second lesson of the seminar Topology: for a Touch Math, taught by Luca Migliorini, University of Bologna. We were without any fear, because we did not imagine that our teacher would introduce the Artin braids saying that they are, in his opinion, the most narrative object of the topology. Since then until today, uninterruptedly, we worked once a week from the after dinner hour until about sunrise, to build braids to represent fairy tales. Although we made a very limited use of the mathematic of Artin braids, the dread of making a blunder in this field could have discouraged us from starting this application, without the helpfullness of Luca Migliorini. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.1. THE LORD OF THE BRAID: EMIL ARTIN
|
The field of braids
was opened in 1925 by the great Austrian mathematician Emil Artin
(Vienna 1898 - Amburgo1962), as a prerequisite to solving very complex
problems in the field of the knots.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.2. WHAT TOPOLOGICAL BRAIDS ARE? |
A topological braid is a tridimensional object, made of a definite number of strings, named curves, three in FIGURE 10. The strings start from and end in two parallel lines, that are not drown in the same figure. The distance between the parallel lines may change without limits, as well as the distance among the curves on the lines. We could think of these curves as made of a material that can be extended and reduced without limits, they can float in the space without merge in each other or intersect each other. The braids are oriented in the space: the parallel lines that delimit them are oriented from left to right, and the cross formed by the strings, without any melting or intersection, as well as a braid of hair, go from the starting bar to the ending bar, and from left to right. The irreversible orientation of the parallel lines and of the crosses is a favourable character to represent a tale, in which an event irreversibly follows another during the time. Let us think of a magic spell, be the spell that sends to sleep for a century the princess Briar Rose, or the spell for which a prince was born in a pig shape: there is always an opposite spell that lets Sleeping Beauty come alive and the prince Pig recover his human shape. There is however an irreversible temporal order between curse and liberation, and there are events of various nature, movements and encounters good and bad, withiut which Briar Rose would go on sleeping and the Prince Pig grunting. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. THE RICH STORY OF A CENTENARIAN FORMALISATION |
The first attempt to formalize fairy-tales date back to the pioneer work by Marian R. E. Cox, Cinderella: Three Hundred and Forty-five Versions (London, 1892); the formalization of fairy-tales has its most fruitful expression with Morphology of the Folktale by Vladimir J. Propp (Leningrad 1928), and it was decisive in the collection and classification of all the fairy-tales motifs by the Finnish School, that gives birth to the monumental work by Antti A. Aarne and Stith Thompson, The Types of the Folktale: A Classification and Bibliography. (Helsinki 1961). The Morphology by Propp, translated and published in the West more than twenty years after the first Russian edition, has crucially influenced the French structuralism, and hence the thought of Jacques Lacan (see: Dmitry Olschansky, 2008, The Birth of Structuralism from the Analysis of Fairy-Tales; accessed July 30, 2011). This wide influence of Propp's morphology is linked with the universal nature of fairy-tales, that are the stories endowed with the height of stability as well as with the height of flexibility. They are the most universal stories because of their diffusion in time and space, and because of the heavy presence of their motifs in our imaginary. In our time they are the narrative structures of many films that get together a worldwide public of children and adults, for example Avatar by J. Cameron (USA 2009). The fairy-tales were similarly told among the lower classes, in the farmyard during the summer or in the cowshed in winter, for a public encompassing children, adults, and old people. The fairy-tales represent the psychic reality, and for this reason they follow the laws that Freud described for the dreams (see the Chapter 7 in The Interpretation of the Dreams [1899]). Much more than night dreams fairy-tales are ruled by the notion of representability, that confers on them a special narrative consistency: they are usable by an almost unlimited public, without age or culture boundary, while night dreams have a private nature, and they often turn out incomprehensible for the dreamer himself. Fairy-tales belong, for their narrative consistency, to the set of stories that comprise short stories, legends, the myths, science fiction or realistic novels. They belong, for their link with psychic reality to the field of the psychoanalytic research. We ought to Bruno Bettelheim the discovery of the importance of fairy-tales in the education and in the terapy of children suffering from a psychic disease, even if his interpretations look outworn (see: B. Bettelheim, The Uses of Enchantment. The meaning and Importance of Fairy-tales, 1976; see also La fiaba come rappresentazione eidopoietica, in A. Gasparini, Aladino e la lampada meravigliosa. Viaggio psicoanalitico; Firenze, 1993). We have always to remember that the fairy-tales are a unit, fascinating for their psychic meaning that works together with a poetic expression. We could think of fairy-tales as of a Janus Bifrons, having a face looking at the unconscious and a face looking at the consciousness. Any interpretation that limit itself to one face, would be partial, unable to catch the specific value of fairy-tales, that is the main reason for their communicative potency as well as for their utility in educational and therapeutic works. A psychoanalyst anlyzing fairy-tales supplied with his interpretative tools, without considering their poetic value, or their language and culture, could offer an effective interpretation, but it would sound arbitrary and unacceptable for scholars not involved in the psychonalytic field. We could effectively interpret fairy-tales by any psychoanalytic theory, just translating fairy-tales' actants and events by the corresponding elements in the choosen theory (see, by A. Gasparini, Se le metafore giocano, 2010). Similarly, a mythologist or a literary critic studying fairy-tales without considering their side linked to the psychic reality, would be unable to understand the particular power of this kind of stories. The up to now proposed formalizations employ linear formulas, or bidimensional tables, that level fairy-tales, being unable to catch their third dimension, depth, that is their perspective play among events and actants, and it is also unable to represent the fourth dimension, time, in which events and actants dive to go on, walking and walking, from a death risk to an happy end. The Artin braids offer a chance to proceed keeping count of the fertility and of the limits of these interpretations. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.1. BRAIDS OF CINDERELLA. GEOMETRICAL REPRESENTATIONS |
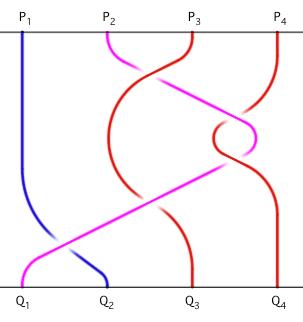
In a braid with n strings (n indicates an ordinal integer number, 7 in the FIGURE 15) L1 and L2 are parallel lines oriented from left to right - the same direction indicated by the arrows. If P1, P2 ... P7 are points of L1, and Q1, Q2 ... Q7 are points of L2, we link each point P to each point Q by curves, oriented from L1 to L2., in our figure from up to down. 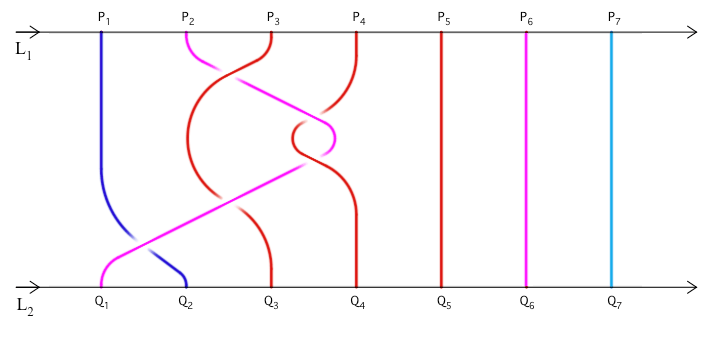 FIGURA 15 The FIGURE
15 is the two-dimensional projection
of a object three-dimensional object, that represents the crosses
suspending the curve that goes past the curve with which it crosses,
and this figure is the first of the four braids of our formalization
of La gatta
Cennerentola
(Basile, 1634).
Each string represents a fairy tale's actant, each cross represents an interplay between two actants. We distinguish four kind of actants colouring their corresponding curves: blue, fatherly
actant;
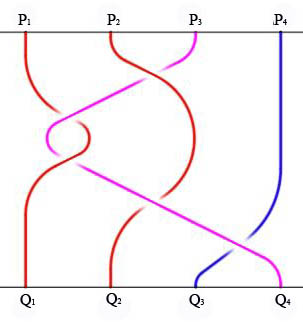
red, motherly actant; sky-blue, filial male actant; pink, filial female actant. The order of the braids that formalize La gatta Cennerentola is 7, in the sense that the fairy tale's characters are represented by 7 curves. In the first braid (FIGURE 15) there are the following actants: 1. the Cinderella's father, fatherly actant (P1-Q2); 2. Cinderella , filial female main actant, (P2-Q1); 3. the first stepmother, motherly actant, that is present since the beginning of the story (P3-Q3); 4. the sewing-teacher, motherly actant, who would become the second step-mother of Cinderella (P4-Q4); 5. the fairy, who would introduce herself in three different analogous shapes, namely a talking little dove, the Dove Fairy and the Date Fairy, with a protective and donor motherly function (P5-Q5); 6. the stepsisters, filial female actants, who act in unison and for this reason are represented by one curve (P6-Q6); 7. the king, filial male actant, who falls in love with Cinderella and plays the same role of the prince charmant who is in other versions of this fairy tale (P7-Q7). In this first braid the curves corresponding to the fairy, the stepsisters and the royal suitor of Cinderella do not intertwine among themselves or with other curves: they figure in the tale meant as a complete set, even if they have no cross in this first braid. The first stepmother, who dies in the second last cross of this first braid, not to come back to life (it may happen in other fairy tales), will figure in the following braids by a curve without any other cross. The parallel lines L1 ed L2 represent the beginning and the end of the fairy tale, or of one of its parts, and they are fixed like the white pages that come before and after the tale. Geometrical limits of the braid, they represent the limits of the story. We could imagine the curves, formalizing the actants, made of an elastic material as well as every topological object, that for this reason might be without limits extended, bent or contracted. The consistency of this material does not allow them the chance to merge or intersect each other: if this could happen we would have operations of cutting - to insert a curve into another curve - or pasting - to merge them. It also means that two curves cannot strat or end with the same point. Two persons meeting themselves, in war or in love, may seem melted being however distinct, as well as our strings that cross themselves, and so they change their position in the order of the curves from left to right, never getting confused one with the other. Freely floating in the space, the curves can never invert their direction from L1 to L2:, that in our braid would mean to walk back. By the braid we formalize just the fabula, that is the temporal sequence of the events introduced by the tale, while we do not represent anything told in flash-backs or flash-forwards, regardless of the importance of events introduced by a flash-back o a flash-forward. By events we mean here the meetings between actants, represented in the braid as crosses between curves. In the mathematical language of Emil Artin the crosses are algebraically expressed bu the Greek letter s, and they are named generators. In fairy tales as braids each generator, leading to a change of the actant's place, make possible for this actant a meeting with another actant, represented by the curve that happens to be at its right after the cross. From the first braid of La gatta Cennerentola (FIGURE 15), we get another braid isolating the part that represents the first four actants, from left to right, with their 5 crosses (FIGURE 16). The captions in the same figure are the captions that we can read in the page that contains the above mentioned topological pattern of the whole tale, costitued by 4 braids (La gatta Cennerentola). Each caption is preceded by two numbers, the first indicating the braid (1 in FIGURE 16, because this is the first braid of La Gatta Cennerentola), the second indicating the generator or cross of the braid (1, 2, 3, 4, 5 in this example).
As we said, in mathematical terms the crosses among curves are named generators. In our formalization we would arbitrarily use the technical meaning of the algebraic term (that is related to the group theory) with the meaning that it has in the natural language, in which generator relates to the idea to give birth, to arouse: in this meaning, in fairy tales as braids, each cross generates the chance of a cross between actants that was before impossible. Just when Cinderella's string intertwined with the string of her first stepmother (1.1; s2¯¹), in the cross that represents the relation of burden characterizing this and almost every version of Cinderella, her string may intertwine with the string of her sewing teacher, with whom Cinderella complains of her stepmother (1.2; s3). Cinderella has now her sewing teacher at her left, and just by a new cross with her she would come again near the string of her first stepmother. Then Cinderella, following the advice of her sewing teacher, would cross with her first stepmother killing her (1.4, s2¯¹). Having eliminated her first stepmother, Cinderella has the string of her father at her left, and she would intertwine with him, in the fifth and last cross of the first braid, persuading him to marry her sewing teacher, who should satisfy her desires in every way (1.5; s1¯¹). Each string, or curve, may intertwine with the curve that is at its right, in two ways, crossing on or under it. In this two-dimensional geometrical representation this option is indicated by a brief break in the string that in a cross passes under another string, we must however remember that no string breaks itself in the three-dimensional space between the two parallel lines. In the algebraic expression a negative exponent indicates the generator where the left string (e.g.: 1.1; s2¯¹, Cinderella) passes under the string that is on its right (e.g.: the first stepmother). The positive exponent, omitted (e.g. : 1.2; s3), similarly represents a cross where a string (again Cinderella) crosses with the string at its right passing over it (here the sewing teacher, second stepmother-to-be). The subscript number of any s indicates the generator, without reference to the starting position of the crossing strings on the parallel L1. The number of the generators is the order number of the braid, given by the number of its strings minus one. In our braid (FIGURE 16) the order number of the braid is 4: we aheve four strings and therefore 4 - 1 = 3 generators. Since the crosses are made by the movement of a string from left to right, the string that is external right cannot cross, having no other string at its right. In this example the string representing the sewing teacher in the start position cannot do any cross, nor the string Cinderella after its first cross with the sewing teacher. If we go back to FIGURE 15, that represents also the actants that do not do any cross in this braid, the order of the braid is 7, being 7 the actants-strings, while the generators could be just 6: in this figure the king, groom-to-be of Cinderella, could not cross any other string, being external right in the braid. The attentive reader could now ask us what may be the meaning of the crossing on or over between two strings in our formalization. This may be the most complex problem that we faced in our research, and we choose a solution to go on, even if it is not satisfactory. Formalizing the fairy-tales we geometrized the chronologically ordered set of the crosses between the characters, trying to give up that kind of dead weight made by any moralistic yardstick, ruling in education and in common sense, as well as every psychologistic yardstick, seen by us as a particular expression of a common moralism, to which the psychoanalyst himself sometimes pay a undue toll. Also symbolism, that is so important to understand the value and the richness of fairy-tales, is totally non influential in this formalization. Coming back to the meaning to assign to the crossing of a string on or under the string at its right in the various generators, it has here nothing to do with any kind of superiority of one of the crossing actants, therefore it does not mean any submission of one actant to the other. At the moment, we were not able to find a better solution than representing the manifest content of the fairy-tales. In any cross the actant string passing on the string of the other actant represents the character that decides, chooses, free agent, that interplay, be it destructive or sheltering, against or for the actant whose string it crosses. Let's give two examples for our first braid of Cinderella, that we can see in their geometric representation on this page (FIGURE 15 and FIGURE 16). For the complete topological scheme (4 braids) see the page dedicated to La gatta Cennerentola. The first generator (1.1; s2¯¹) formalizes the cross between Cinderella and her first stepmother. Balile tells us that this stepmother, not standing Cinderella, frightend her by bad and scowling faces: "...giving her odd, evil and nasty looks, so that the poor girl was terrified...". We also know that her stepmother had decided to burden Cinderella, who, on her side, was subjected to this harassment. Therefore the string corresponding to the first stepmother passes on the string corresponding to Cinderella. The matter is here a mother-daughter conflicting relation, destructive enough to put one of them to death: the manifest content put the whole blame for this first cross on the first stepmother, but we know that unconsciously the main character chooses a masochist position with this motherly figure of her, supporting her aggressiveness. A fairy-tale is a story of various actants, and if we read it as a dream we see these actants as parts of the same subject, who may know some of them as his own, while he puts some unpleasant or simply unknown parts of his on other characters. Cinderella does not represent any specific maid, but the female component of any subject. She represents any subject's receptivity, capacity of nourishing and rising , to wait silently for something to grow up, without knowing what it will be. In this sense the destructiveness of the burdening stepmother, as well as the masochism of Cinderella - told as innocent docility - may belong to any the subject. We are looking the first braid of the seventeenth-century text, where the destructiveness of the main character comes out in no uncertain terms with her homicidal violence, by which Cinderella - with her sewing teacher partenr in crime - hopes to get a stepmother that she could rule, a new mother who should anyway satisfy her. Cinderella's power of persuading her father to marry her sewing teacher suggests her incestuous position: she is the ideal partner of her father, who looks ready to grant all her desires. At the beginnig we can read that He had an only daughter, so dear to him that he saw with no other eyes than hers. In the second generator the string of Cinderella passes on the string of her sewing teacher (1.2, s3), because Cinderella on her own intiative moans with her about her first stepmother, while the string of the sewing teacher passes on the string of Cinderella in the third generator, when the sewing teacher suggests her the way to get the first stepmother out of Cinderella's way once and for all (1.3, s3). In Artin braids the left string always moves to right, while in the fairy-tale as a braid we might have the feeling that Cinderella, so to speak, would go back from the sewing teacher to the first stepmother, to kill her (1.4, s2¯¹). Then she would go back to her father, to persuade him to marry her sewing teacher (1.5, s1¯¹). The algorithmic expression of this braid is however corresponding with the notation by Artin. No sensible notation, widely many-sided, should try to exhaust the meaning of a fairy-tale, as well as no biological theory can exhaust the meaning of life. The function of a formalization is not hermeneutic, it does not try to tell what a fairy-tale would mean, but to geometrize it. It aspires to describe variants and constants in the fairy-tales, and therefore to know the connection among distinct versions of the same fairy-tale, and among different fairy-tales, that may have one or more common motifs. A formalization may be worthwhile if it results useful in this sense, to detect why many quite different versions are after all Cinderella, to understand why it is so easy to recognize its type. We would now hypothesize that different versions of the same fairy-tale contain a peculiar part formalizable by a homeomorphic braid that typifies them. We consider two braids homeomorphic when we can transform one into the other moving their strings without any cut or paste. In this sense we observed stories' motifs that sound different but present a homeomorphism by this formalization, while similar motifs cannot be reduced one to another by a continuous deformation of their strings. The results of our research are actually modest, but they are enough to formulate the hypothesis just enunciated, that we are going to define by an example. Before giving this example we have however to tell something about other two sides of our formalization. The first of them pertains to the succession of the actants on the line L1, that represents the beginning of the fairy.tale or one part of it. The second side pertains to the partition of the fairy-tales in two or more parts formalized by distinct braids. As well as for the standard we adopted to decide when a string representing an actant should pass on or under another string in any generator, it was the story that led us to choose a method to decide the succession of the actants on the line L1, and to determine the number of braids required to formalize a fairy tale. The disposition of the braids from left to right, on the line L1, corresponding to the actants, depends on the need to represent their crosses in the chronological order; the generators in each braid are therefore ordered from L1 to L2 . Looking at FIGURE 16 we can observe that the first generator is set up by the string representing Cinderella and the first stepmother, that respectively start from P2 and P3. If the strings representing the first stepmother would start from P2 and the braid of Cinderella would start from P3, after the first cross the strings corresponding to Cinderella should be on the left of the string of her first stepmother and on the right of string representing her father: it would be impossible to formalize the following cross told by this story, that happens between Cinderella and her sewing teacher, second stepmother-to-be. The same thing can be observed about any following cross of this braid.
When we admit that it is possible to represent the cross among actants just choosing a suitable sequence of the strings on L1, (e.g.: father, Cinderella, first stepmother, sewing teacher), we can see that in FIGURE 17, the braid is specular to the braid in FIGURE 16, the order of the strings on L1 is inverted (sewing teacher, first stepmother, Cinderella, father) and the follow the same order. The algebraic expression of the braid in FIGURE 16: s2¯¹ s3 s3
s2¯¹ s1¯¹
corresponds to this expression if the braid in FIGURE 17: s2 s1¯¹ s1¯¹
s2 s3
.where the exponent of the generators are inverted. In both these braids the strings of the actants however pass on or under each other in the same way. We could see that the strings of the fairy, the stepsisters and the principe, that we did not represent in FIGURE 16 and 17, to get simpler examples, are shown in FIGURE 15, even if those actants do not yet take part in the story. In the following braids geometrizing La gatta Cennerentola, we could see the red string corresponding to the first step-mother, killed in the first braid, who is not going to do anything els in the story; in other fairy-tales it may happen that a died character would become alive. This representation is comparable to a theatre company, whose actors are however there, even behind the backstage, before coming on the stage, as well as when they closed their part. The last point in this introduction to Fairy-tales as braids, concerns this: a fairy-tale of the type of our La gatta Cennerentola, that can be seen as the recorded ancestor of every following Cinderella, is formalized by 4 braids. Why a single braid should not be enough to represent all the actants' interplays, that are the braid's generators? We can give the same answer we proposed for the previous point, about the order of the strings on L1: we close a braid when the position of the actants at one point of our formalization stops tthe possibility to go on formalizing the following interplays. Concerning this we know that any of our braids could be improved: these first results are offered as a example of our research. We know that we are going to rectify them as well as we did many times. The number of braids that form the topological scheme of a fairy-tale, in its geometrical and algebraic expression, is however the lowest number of braids that we need to formalize in chronological the set of the actants' interplays, that are the generators of their braids. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.2. BRAIDS OF CINDERELLA. ALGEBRAIC EXPRESSIONS |
We presented the first braid of La gatta Cennerentola, describing both its pattern and its algorithm. We call topological scheme the set of the braids formalizing a fairy-tale, that is composed by a number of braids from 1 to 7 in the stories that we up to now formalized. La gatta Cennerentola is formalized by 4 braids, that are shown in the page that we already quoted. We applied to the algorithms composing our topological scheme the associative property, to get simpler algorithms, taht we call paradigm of the fairy-tale. The number of the geometrical braids and of the algorithms is obviously the same both in the topological scheme and in the paradigm of a fairy-tale (4 in La gatta Cennerentola). As well as the paradigm of a verb gives the basic elements to conjugate it, the paradigm of a story gives the basic elements of the transformative interplays among its actants. And as well as the paradigm of a verb does not enclose the whole range of its verbal forms that we could find in a speech, the paradigm of a fairy tale would not enclose the wole range of generators that formalize all the actants' interplays of that story.
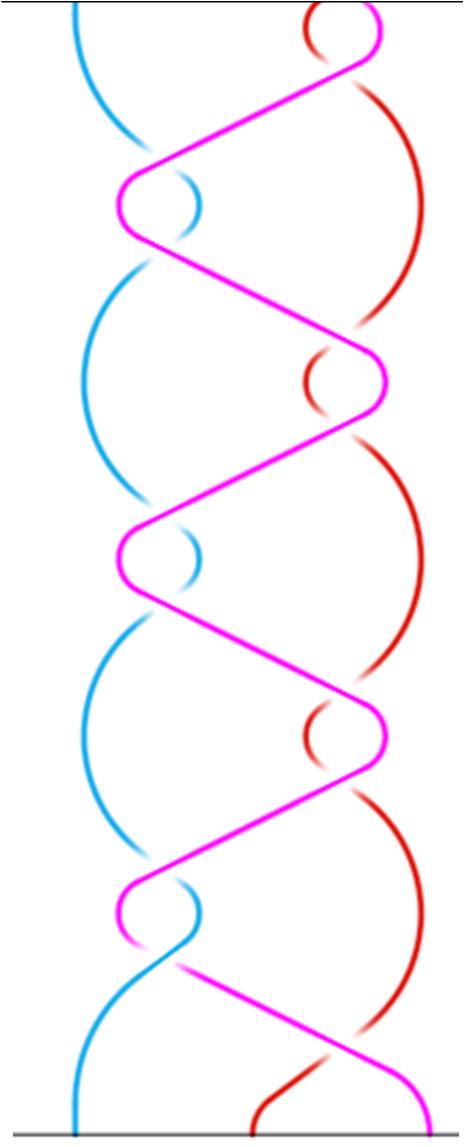
To explain what is the meaning of the paradigm of a braid, how we can get it, what potential it could have in the study of fairy-tales, of their variants and constants, we would go on by an example, taht we draw from the braid 3 of La gatta Cennerentola. We get a new braid, shown in FIGURE 18, that we extracted from the whole braid 3. The order number of the captions and the subscript number of the generators corresponds to the numbers of the whole braid 3.
La gatta
Cennerentola is magically dressed by the Date Fairy, then she
goes to the promenade where there is the king, then the king falls in
love with her.
And then Cinderella
flees, vainly tailed after the king's order, and finally she asks to be
undressed by the Date Fairy to go back near the fireplace, as if she
would never have left it. This same set of interplays among three
actants, formed by 4 generators (s2¯¹
s1¯¹
s1
s2) repeats itself a second time. It
repeats itself for a third time, but only the first, the second and the
fourth generators are the same: in the third cross between the strings
of Cinderella and the king, Cinderella passes under the string of the
king, while in the two previous sets she passed on it (s2¯¹
s1¯¹
s1¯¹
s2) .
In the first and second identical set the determination of Cinderella
to flee, preponderated over the determination of the king to catch her,
to know her name and her address. In the third set the determination of
Cinderella to flee is overturned by the determination of the king,
because in this case he gets her shoe, that is, by the way, the
fairy-tale most famous magic object in the world. This
transformation puts an end to the repetition of the
appearing/concealing performance of the main character. The elation of
the king in this ancient Cincerella story is a poetic expression of the
importance of the new generator (3.17: s1¯¹):
The king, holding it in
his hands, said: « If the basement is so beautifukl, what must
the building be? O beautiful candlestick, that held the candle that
burns me! O trivet of the beautiful boiler where life is boiling! O
beautiful float linked to the line of Eros, by which he fished my soul!
There, I hold you and I hug you, and if I cannot reach the plat, I
adore the roots, and if I cannot get the capital, I kiss the basement!
You already were the stone of her white foot, and now you are the snare
of my black heart; she who tyrannizes my life was by you higher one
span and one half, and as much rises the sweetness of my life, while I
am looking at you and holding you".(For the full Italian text see La
gatta Cennerentola;
In any version of Cinderella story we can see the same intertwining
that we have represented for La
gatta Cennerentola in FIGURE 18. We present here
a table containing this and other three variants of the story. The
titles are linked to their complete topological schemes.the English translation is ours; for the full English text see Cinderella Cat)
In the topological schemes of these four versions we can see that the narrative variants of each story show the recurrence of the generators that we here highlighted. Let's go back to the algorithm of the braid we got from the third braid of La gatta Cennerentola (FIGURE 18): s2¯¹ s1¯¹ s1
s2 s2¯¹ s1¯¹ s1
s2
s2¯¹ s1¯¹ s1¯¹ s2
Let's now start to reduce this algorithm to get the paradigm of the same braid. We first colour red the pairs of generators to reduce that represent interplays between Cinderella and the Date Fairy, we colour blue the pairs of generators to reduce that represent interplays between Cinderella and her royal suitor: s2¯¹
s1¯¹
s1
s2
s2¯¹
s1¯¹
s1
s2
s2¯¹ s1¯¹
s1¯¹
s2
Then we cancel these coloured pairs of generators since they are formed by sigma having opposite exponents | s1¯¹ s1 | and | s2 s2¯¹ |, and we get the following formula, where we colour blue the pair of generators representing the interplay between Cinderella and the king, when he gets one of her schoes: s2¯¹
s1¯¹
s1¯¹
s2
We finally apply the associative property to the blue sigma to get the paradigm of this braid: s
Let's now go from the algebraic expression to the correspondent geometric braid (FIGURE 18). We should remember that it is the bi-dimensional figure of a three-dimensional object, therefore the strings should be seen as made of a material that makes them extendable and compactable without limits. Let's now imagine to pull up by four moves the pink string (representig Cinderella), doing four moves as in FIGURE 19. Reducing the lengt of the super-elastic pink string and both the red and the light blue ones, we can get the braid in FIGURE 20; then let's go on moving and reducing the strings in FIGURE 20 we can get the braid in FIGURE 21, without any cut or paste: all these braids (FIGURE 18, 19, 20 and 21) are homeomorfic. Since topology is a more tactile than visual geometry, we could more easily understand this homeomorphism by constructing the braid. We could start spinning three strings on a little carboard like in FIGURE 18, moving and crossing them. Then we should pull up them and reduce their length, so to get FIGURE 19 and finally FIGURE 20. This homeomorphism is pregnant with many possibilities to study constants and variants in fairy tales. We made so many braids by real strings and pins for over one year before being able to understand them and their properties by simple bi-dimensional draws, that we consumed meters and meters of coloured strings.
 As we said, the braid in FIGURE 21 is
homeomorphic to the others. and it is, as well as FIGURE 20,
the geometric expression of the following algorithm, quoted above: As we said, the braid in FIGURE 21 is
homeomorphic to the others. and it is, as well as FIGURE 20,
the geometric expression of the following algorithm, quoted above:s2¯¹ s1¯² s2 What is present in any version of Cinderella is this paradigm: it is what enables us to say "This is Cinderella!" listening or reading all of its different versions. The topological schemes of the different versions of Cinderella, containing all the generators, that represent all the interplays among the actants of the stories, scheme Quel che è presente con evidenza in tutte le versioni di Cinderella è il paradigma, show more differences between them. Lets speak now about the content of the fairy-tale. The generators that we cancel reducing the algorithm of the topological scheme, getting the reduced algorithm that we call paradigm, concern two kinds of crosses: between Cinderella with the fairy by whom she dresses and undresses herself, and between Cinderella and the king, to whom she appears and whom she eludes. We saw that in the Cinderella by Walt Disney the repetition of this two double crosses is missing: Cinderella is dressed just once by the fairy god-mother; she goes joust to one ball, after which she looses one of her shoes, and then she finds herself ragged because the her magic spell ends at midnight. Perrault tells that Cinderella is dressed by the fairy and goes to the ball, then she finds herself twice ragged after mindnight strokes. Basile and the Grimm tell that Cinderella thrice magically dress herself, and thrice undressed herself. In these two versions she appears thrice to his royal highness, eludes himself the first and the second times, and on the third she leaves one of her shoes behind herself. The chianiello told by Basile, the Grimm's golden little shoe, the vaire, glass or christal shoe of Perrault, they all are the most famous fairy-tale object in the world. That is a metonomy for Cinderella herself, it belongs to her, and it will be enough to find and identify her. In this formalization no magic object is represented, but we would hypothesize that these braids may enlighten their importance. The wide presence of the little shoe of Cinderella, as well as of the Aladdin's lamp in the worldwide imagination deserve a rigorous attention. It does not seem an intelligent attitude to get rid of them, as if they would 'simply' belong to a kind of low education. In every version of Cinderella, her hiding, that is forced by her stepmother to serve her stepsisters without going to the ball, is not over when she gets the help of the fairy: she chooses to hide herself again in Basile and Grimm, as well as in many popular versions. The hiding of Cinderella comes to an end when her royal suitor actively plays his desire catching the little shoe that represents her owner: it fits only Cinderella Cinderella is the fairy-tales actant most famous in the world, and her shoe surpasses even the Aladdin's lamp. It is usually seen as a very little shoe, but the chianiello told by Basile, as well as the shoe of many popular versions, is not especially little or big, it is simply perfect for her foot. It is a particular case that the golden slipper of Brothers Grimm cannot fit the too big shoes of the stepsisters, as well as the glass slipper of Perrault and Walt Disney (for an interpretation of this particular case, that is the most famous, see, by A. Gasparini, La luna nella cenere).  We could better
understand the
importance of this magic and symbolic object seeing its links to the
crosses among Cinderella, the fairy and her groom-to-be, represented by
the generators of our braids: just when the king gets Cinderella's
slipper he would stop the fleeing Cinderella. The charm of Cinderella
who twirling at the ball, her lightness that makes her uncatchable when
she flees, by her magic coach that nearly spreads its wings to elude
the king's servant in Basile, by her acrobatic jumps to go back home,
through the dovecot or the peer tree, so that the Grimm's prince could
not reach her, all these sign of grace and nimbleness are present in
the little glass slipper that everyone remembers. We could better
understand the
importance of this magic and symbolic object seeing its links to the
crosses among Cinderella, the fairy and her groom-to-be, represented by
the generators of our braids: just when the king gets Cinderella's
slipper he would stop the fleeing Cinderella. The charm of Cinderella
who twirling at the ball, her lightness that makes her uncatchable when
she flees, by her magic coach that nearly spreads its wings to elude
the king's servant in Basile, by her acrobatic jumps to go back home,
through the dovecot or the peer tree, so that the Grimm's prince could
not reach her, all these sign of grace and nimbleness are present in
the little glass slipper that everyone remembers. A glass or christal shoe is quite unrealistic: if Cinderella would dance or run, or even walk wearing glass shoes, she would break them hurting her feet. By this irreal wonder the poetry of the fairy-tales represent a dream, made by a nimbleness and a charm without limpits, together with their distance from any realistic translation. These impossible an poetic material could come from an happy blunder made by Perrault, who wrote verre, glass, for the word that in the popular oral version heard by him was vaire, homophonic to verre. Vaire was a kind of soft fur, by which preciuos shoes were made. We think that the symbol of Cinderella's famous slipper, as well as every symbol, may be really understood only in the context it belongs to. Fairy-tales as braids may be a rigorous method for this understanding. Audrey Hepburn and Fred Astaire in Funny Face (in Italian: Cenerentola a Parigi) Stanley Donen, USA 1957 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. FAIRY TALE GEOMETRIES FOR EXCLUSIVE SLIPPERS  FIGURE 22
Sandals of Cinderella
(value 2.000.000 dollars) worn by the singer Allison
Krauss in the Oscar Night, 2004
|
Which meaning could we now assign to the repetitions that are in so many versions of Cinderella, to the cross between her and the fairy, and to her and the royal groom-to-be? Why is almost never enough for this story what ony one magic dress, only one ball, only one escape? We do not know another version but Disney's one, missing the repetition of the motif formalized by FIGURE 18. The generators cancelled reducing the algorithm of the topological scheme (FIGURE 18) by the moves shown in FIGURE 19, (their mathematical name is Reidemeister moves), represent pair of crosses where the movement come from the activity choosen and acted by only one character. Cinderella asks the fairy to dress and to undress her to go to the king's promenade and to go unknown back to the home fireplace in Basile and in Grimm. Her string passes on the string of the motherly fairy when she dresses and when she undresses herself. Cinderella decides in both these versions to appear to the king and to escape him. No bond ties her to go back at a given time or to flee in these versions and in many ancient or popular versions. It happens in the widspread versions of Perrault and Disney, where the motherly fairy decides to dress and to undress Cinderella: in the correspondent braids it is the string representing the fairy that passes on the string of Cinderella. By our Reidemeister moves we can solve these crosses as well those between Cinderella and her royal suitor till the interplay that formalizes the moment when he catches her slipper. Here the groom-to-be decides and acts: his string now passes on Cinderella's string, because his intention prevails against her flight, his desire to find her prevails against her hiding, when he catches the golden or glass slipper. There are interplays, and crosses, named generators in the braids that formalize the fairy tales, that may be solved in the geometrical braids, and similarly cancelled in the correspondent algorithms. There are other generators that cannot be solved or reduced: these are the transformative generators in the fairy-tales. They formalize pairs of crosses between actants when both of them will or desire, and realizes an action: a crossing string passes on and under the other crossing, and here we cannot comb their intertwining. This may be the most interesting meaning in this formalization: every transformation, every story that tells a trasformation of its characters, entails a meeting coming from the desire and the action of both the characters that cross themselves. We could see the repetition, the generators that we can reduce, as a preparation to this transformative cross. Is not the same in our life? Few important things realize themselves at one's first attempt. There are fairy tales, whose braids we are going to put on line, where the main female and male actans marry themselves at the beginning of the story. These tales go on through the quick lost of this happy marriage, and the long way to get it back. They tell how many crosses are necessary to get something precious, with a long way, with pain, working, efforts, they tell how we have to gain back what had been easily got. Many crosses are needed: with fatherly and motherly actants, adverse and propitious, with sisters or brothers adverse and propitious, with actants of the opposite gender, that find and loose themselves and find themselves again, towards an happy hand that is hard to be catch. Cinderella, whose name may be gatta Cennerentola, Cendrillon, Aschenputtel, flees nimble and light, with the same grace she has twirling in the dance hall of the royal palace. Why does she flee away? Why she does not reveal her name and address to her royal suitor, who would marry her since the moment he saw her? Why does she ask wonderful dresses to undress herself and go back unknown to the cinder of the fire-place? Why should her stepmother and her stepsisters not know that the beautiful maiden loved by the king is the girl who sits on the fireplace, rugged and dirty with cinder? What is the repetition, that Sigmund Freud called Thanatos, compulsion to repeat? If gatta Cennerentola would have had a freudian psychoanalyst, if she woud have gone to see him between one and another ball, between one and another dress-changing, would not she be regarded as an hysteric? Sure her psychoanalyst would have asked her why she went on asking to be dressed and undressed by the fairy, given that her royal suitor was ready to marry her? We know that it is unuseful, if not detrimental, to interpret a fairy-tale, as well as any work of literature, as if its main character, or its author himself, would be patients. It is unuseful, if not detrimental, to think that the meaning of a fairy-tale may be simple to understand. Fairy tales have crossed many centuries, never loosing its freshness, they go with their poetic life through many borders, nimble enough to be told in illiterate communities as well as in refined circles (Giambattista Basile belonged to one of them) or sumptuous courts (Charles Perrault wrote his tales for the Sun King), or the film industry of Walt Disney. No application of any psychoanalitical theory, no even refined hermeneutic can easily understand them or exhaust their meaning. Cinderella has an important place in the worldwide imagination. In 1892 Marian E. R. Cox published her collection made of 345 versions; if today we type Cinderella by Google we get 19.000.000 results, 2.900.000 typing Cenerentola, 1.100.000 with Cendrillon, 888.000 with Aschenputtel. It is easy to take a look at the huge number of sites that provide Cinderella weddings, with coach, castle for the reception, dresses, favors and decorations. One can get many kinds of Cinderella's shoes, often made by a plastic material that looks like glass. We can see a pair of Cinderella's sandals studded with diamonds, whose value is literally fabulous. were un paio di sandali tempestati di diamanti, di un valore letteralmente favoloso (FIGURE 22). The braid in FIGURE18, that by the Reidemeister moves shown in FIGURE 19 becomes the homeomorphic braids shown in FIGURES 20 and 21, typifies every version of Cinderella that we know, at the moment we show this only in the four versions we chose. Cinderella's story shoud mean something very important about the feminine. To understand it may help us to give reason of its function in the collective imagination, not only in the infantile one. Therefore we hypothesize that the braid we are speaking of represent this. The fairy tale of Cinderella tells the mourning of a young woman who lost her positive motherly figure. Instead of her she gets a burdening stepmother and stepsisters that take her place in the love of the father. It tells something about the painful and lonely darkness of the protagonist, as well as of the same experience of any person who would read or listen to it. A feeling of dirtiness is present, tied to an unconscious fault, represented by the rags and the cinder. Cinderella can only clean the house, her house, that represents her mother and her own body, to mend the tear of the loss. The long time of the mourning, of which no fairy tale gives a measure, comes to an end when the main character's desire to show her beauty comes out of this darkness. To grant this desire Cinderella has to get a new form, a new dress: dress means identity. This transformation is not the sum of some elements, even if it needs many elements. We shoud think of it as of the blossoming of a flower, a natural event belonging to the domain of nature, that the ancient Greeks called fusij. This transformative event needs a human work that resembles to a gardener's cares, and it need favorable conditions of light and warmth. This concept requires a longer treatment, that we postpone to a next time. In this context we would observe that this transformation realizes itself by a set of crosses between Cinderella and the fairy and between Cinderella and her royal suitor. Cinderella gets from the fairy wonderful gifts, she can show her female grace by gifts coming from a motherly figure. Let's see these gift in our fur versions: in Basile we see the date fairy, coming from the tree that Cinderella grew; in Grimm we see the hazel tree grown on her mother's grave that Cinderella watered by her tears, in Perrault and in Disney we see the fairy godmather. Her female grace enamour the prince, and the repetition could be understood as a sequence of moments that confirm and consolidate the whole blossoming of Cinderella. The fairy tale could express by these repetitions the time lenght of the event, that cannot realize itself by just one beat. The tale of this blossoming is a chance for any reader or listener to feel the same experience in himself. In a different setting and degree, we deal with the same experience when a transformation happens. It is an experience of which we can speak just after its fulfilment, even if it is hard to consider really fulfilled anything in a human experience. How we can make this experience of blossoming visible, how can we tell it or depict it? How could we understand this happy end, pointing the vitality of a path, without seizing its duration? Cinderella's story tells us that the female blossoming needs two relations, alternating and repeating themselves, between the protagonist and a motherly donor character, and between her and the male character. It tells us that two desires have to emerge intertwining themselves: to get identity both from the mother and from the male's desire. If a fairy mother grants her desire of a wonderful dress, Cinderella can go where she wants: where the desire of a prince or a king grants her beauty. After her dark mourning, after the dirty given by an unconscious fault, after having experienced the bad mother that comes when the first one is destroied, the good mother comes back. The movement of the string that represents Cinderella in our braid (FIGURE 18), repeatedly going from the fairy to the king, and from him to the fairy, prepares the possibility to reach an adult fruitful position. Cinderella flees to be able to come back, she appears to hide herself, she conceals herself to shine. Her slippers, made by vaire or by verre, by gold or glass, very little or just fitting her foot, have a meaning more true than any shoe, because it is impossible to wear them: and just wearing them Cinderella can twirl in the castle's dance hall. Who loves the luxuriant richness of the symbols would find them untouched and clearer after having understood these entertwinings. These braids formalize just the necessary meetings, the crosses betwenn young and old actants, that leave or arise the throne, that leave or find their parents, fighting and loving themselves. They tell a texture, they weave a cloth, where the arbitrariness of any hermeneutic gives place to a moving geometry that gives us the chance to see the fairy-tales actants as strings moving and crossing in the space. The desire to understand the fairy-tales, the reason of their vitality, the fertility of their psychoanalytical use both in the education and in the care of children, the feeling of their rigorous structure, that works together with their poetic nimbleness, leads this research. It tries to answer to a question asked by the great topologist René Thom: We can consider the classical Euclidean geometry as a magic: at the cost of a
minimal distortion of appearances (the point without any
extension, the straight line without any thickness...), the merely
formal language of geometry adequately describes spatial reality. We
might say that geometry is a successful magic. I would enunciate the
reciprocal: is not necessarily every magic a geometry, inasmuch as it
is successful? (René
Thom, Stabilità strutturale
and
morfogenesi. Saggio di una teoria generale dei modelli. Torino:
Einaudi 1980; p. 15, n. 4; English translation is ours)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
AKNOWLEDGEMENTS |
Acknowledgements are due to Luca Migliorini, mathematician, for the open-mindedness with whom he introduced braids and answered our questions; the teachers that attended this year and last year to the seminars about fairy-tales promoted by the Assessorato all'Educazione, Comune di Firenze, for their interest; Antonio Maiolino, psychoanalyst and headmaster of the Centro Paul Lemoine, Scuola di Specializzazione in Psicoterapia, Sede di Napoli, for his confidence, the students of the Scuola di Specializzazione for their attention and their desire to go into more depth; Patrizia Cammunci and Antonello Luigi Armando, psychoanalysts, for their precious support; Antonello Sciacchitano, psychoanalyst, for his radical criticism; Noemi Rossi and Stefano Gorini for the care they reserved to the data processing of the braids; our friends, who listened to us with patience and curiosity, looking at our first braids made by coloured little ropes. We are grateful to them all, for their embarassing questions and critical suggestion, not less than for their generous attention. |